Aleatorische Unsicherheit

Aleatorische Unsicherheit bezieht sich auf die inhärente Zufälligkeit der Daten, die nicht erklärt werden können (Aleatorbezieht sich auf jemanden, der die Würfel auf Latein würfelt). Beispiele für Daten mit aleatorischer Unsicherheit sind laute Telemetriedaten und Bilder mit niedriger Auflösung oder Social-Media-Text. Sie können von der aleatorischen Unsicherheit annehmen 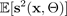, die inhärente Zufälligkeit, entweder konstant zu sein (homoskedastisch) oder variabel (heteroskedastisch), als Funktion der erklärenden Eingabevariablen.

Homoskedastische aleatorische Unsicherheit

Homoskedastische aleatorische Unsicherheit, wenn 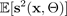ist konstant, ist der einfachste Fall und tritt häufig in der Regression unter der Modellierungsannahme an , wobei , wobei ist die Identitätsmatrix und ist ein konstanter Skalar. Es ist sehr restriktiv, ein konstantes aleatorisches Risiko anzunehmen - davon auszugehen, dass Lärm zu einer Antwort ist unabhängig von der erklärenden Variablen und konstant — und reflektiert selten die Realität. Viele Phänomene in der Natur weisen keine ständige Zufälligkeit auf. Zum Beispiel ist die Unsicherheit über Ergebnisse in physikalischen Systemen, wie Fluidbewegung, normalerweise eine Funktion der kinetischen Energie. Betrachten Sie den Kontrast zwischen dem turbulenten Wasserfluss eines großen Wasserfalls und dem laminaren Wasserfluss eines dekorativen Brunnens. Die Stochastizität (Zufälligkeit) der Flugbahn eines Wasserteilchens ist eine Funktion der kinetischen Energie und daher nicht konstant. Diese Annahme kann zum Verlust wertvoller Informationen führen, wenn Beziehungen zwischen Zielen und Inputs modelliert werden, die ein variables Rauschen aufweisen, und kann nicht mit den beobachtbaren Informationen erklärt werden. Folglich reicht es in den meisten Fällen nicht aus, homoszedastische Unsicherheit anzunehmen. Sofern bekannt ist, dass die Phänomene homoszedastischer Natur sind, sollte das inhärente Rauschen als Funktion der erklärenden Variablen modelliert werden , wenn es so sein kann.

Heteroskedastische aleatorische Unsicherheit

Heteroskedastische aleatorische Unsicherheit besteht darin, wenn wir die inhärente Zufälligkeit innerhalb von Daten als Funktion der Daten selbst betrachten aus. Um diese Art von Unsicherheit zu berechnen, durchschnittlich man einen Stichprobensatz der vorausschauenden Varianz:

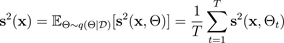
mit 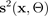wird von einem BNN geschätzt. Das Erlernen der aleatorischen Unsicherheit während des Trainings ermutigt BNNs, die inhärente Zufälligkeit in den Daten einzukapseln, die nicht erklärt werden können. Wenn es keine inhärente Zufälligkeit gibt, sollte zu Null neigen.