Die vorliegende Übersetzung wurde maschinell erstellt. Im Falle eines Konflikts oder eines Widerspruchs zwischen dieser übersetzten Fassung und der englischen Fassung (einschließlich infolge von Verzögerungen bei der Übersetzung) ist die englische Fassung maßgeblich.
Zerlegung von Unsicherheit
Bayessche neuronale Netze (BNNs) ergeben eine prädiktive Verteilung
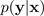, die eine Reihe verschiedener Vorhersagen bietet, anhand derer Sie die Varianz abschätzen können, d. h. die gesamte prädiktive
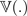Unsicherheit.
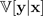Die gesamte prädiktive Unsicherheit kann mithilfe des Gesetzes der totalen Varianz in diese beiden Unsicherheitskomponenten aufgeteilt werden:
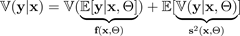
Der Erwartungswert
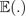einer Zielvariablen
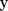wird bei Eingabe
- und Zufallsparametern
, die eine BNN spezifizieren
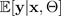, von einer BNN mit einer einzigen Vorwärtsausbreitung geschätzt und als bezeichnet.
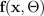Die Varianz des Ziels bei gegebenen Eingabe- und Zufallsparametern wird
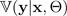ebenfalls von der BNN ausgegeben und als bezeichnet.
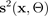Somit ist die gesamte Vorhersageunsicherheit die Summe dieser beiden Zahlen:
-
Die Varianz der vom BNN vorhergesagten Mittelwerte
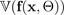— die epistemische Unsicherheit -
Der Durchschnitt der vom BNN vorhergesagten Varianz — die aleatorische Unsicherheit
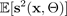
Die folgende Formel zeigt, wie die Gesamtunsicherheit gemäß (Kendall und Gal 2017) berechnet wird. BNNs Eingabe
, Generierung einer zufälligen Parameterkonfiguration und
Durchführung einer einzigen Vorwärtsausbreitung durch das neuronale Netzwerk, um einen Mittelwert
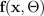und eine Varianz auszugeben.
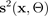Wir bezeichnen eine zufällige Generierung oder Simulation mit ~. Mit Fixed
können Sie diesen Vorgang
viele Male wiederholen, bis Sie ein Set erhalten:
Diese
vielen Stichproben
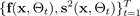liefern die notwendigen Statistiken, um Unsicherheiten zu ermitteln. Sie können dies tun, indem Sie die epistemische Unsicherheit und die aleatorische Unsicherheit getrennt schätzen und dann ihre Summe nehmen, wie bereits in der ersten Gleichung in diesem Abschnitt gezeigt.
