Die vorliegende Übersetzung wurde maschinell erstellt. Im Falle eines Konflikts oder eines Widerspruchs zwischen dieser übersetzten Fassung und der englischen Fassung (einschließlich infolge von Verzögerungen bei der Übersetzung) ist die englische Fassung maßgeblich.
Aussteiger in Monte Carlo
Eine der beliebtesten Methoden zur Schätzung von Unsicherheiten ist die Ableitung prädiktiver Verteilungen mit Bayesschen neuronalen Netzen. Um eine prädiktive Verteilung zu bezeichnen, verwenden Sie:
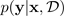
mit Target
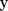
, Input und
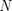vielen Trainingsbeispielen
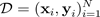. Wenn Sie eine prädiktive Verteilung erhalten, können Sie die Varianz untersuchen und Unsicherheiten aufdecken. Eine Möglichkeit, eine prädiktive Verteilung zu lernen, erfordert das Erlernen einer Verteilung über Funktionen oder, entsprechend, einer Verteilung über die Parameter (d. h. der parametrischen Posterior-Verteilung).
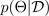
Die Monte-Carlo-Dropout-Methode (MC) (Gal und Ghahramani 2016) bietet eine skalierbare Methode zum Erlernen einer prädiktiven Verteilung. MC-Dropout funktioniert, indem Neuronen in einem neuronalen Netzwerk nach dem Zufallsprinzip ausgeschaltet werden, wodurch das Netzwerk reguliert wird. Jede Dropout-Konfiguration entspricht einer anderen Stichprobe aus der ungefähren parametrischen posterioren Verteilung:
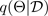
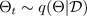
wobei dies einer Dropout-Konfiguration oder, gleichwertig, einer Simulation ~
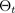entspricht, die anhand des ungefähren parametrischen Posteriors
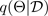entnommen wurde, wie in der folgenden Abbildung dargestellt. Die Stichprobenziehung aus dem ungefähren posterioren Bereich
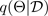ermöglicht die Monte-Carlo-Integration der Wahrscheinlichkeit des Modells, wodurch die prädiktive Verteilung wie folgt aufgedeckt wird:
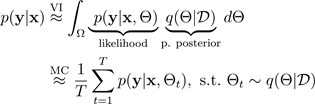
Der Einfachheit halber kann angenommen werden, dass die Wahrscheinlichkeit nach Gauß verteilt ist:
wobei die Gauß-Funktion durch die
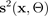Parameter Mittelwert
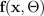und Varianz
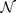spezifiziert wird, die durch Simulationen mit dem Monte-Carlo-Dropout BNN ausgegeben werden:
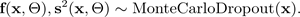
Die folgende Abbildung zeigt den MC-Dropout. Jede Dropout-Konfiguration erzeugt eine andere Ausgangsleistung, indem Neuronen bei jeder Vorwärtsausbreitung nach dem Zufallsprinzip aus- (graue Kreise) und wieder eingeschaltet (schwarze Kreise) werden. Mehrere Vorwärtsdurchläufe mit unterschiedlichen Dropout-Konfigurationen ergeben eine prädiktive Verteilung über den Mittelwert p (f (x, ø)).
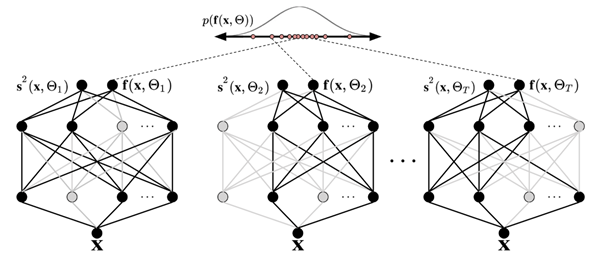
Die Anzahl der Vorwärtsdurchläufe der Daten sollte quantitativ bewertet werden, aber 30-100 ist eine angemessene Spanne, die berücksichtigt werden sollte (Gal und Ghahramani 2016).
