Cadena de espín interactiva Arreglo Interacción Campo de conducción AHSprograma Se ejecuta en un simulador local Analizando los resultados del simulador Corre Aquila QuEra QPU Analizando los resultados QPU Siguientes pasos

HolaAHS: Ejecute su primera simulación hamiltoniana analógica

Esta sección proporciona información sobre cómo ejecutar su primera simulación hamiltoniana analógica.

Cadena de espín interactiva

Como ejemplo canónico de un sistema de muchas partículas que interactúan, consideremos un anillo de ocho espines (cada uno de los cuales puede estar en los estados «arriba» y «abajo»). Si bien es pequeño, este sistema modelo ya presenta un puñado de fenómenos interesantes relacionados con materiales magnéticos de origen natural. En este ejemplo, mostraremos cómo preparar el denominado orden antiferromagnético, en el que los espines consecutivos apuntan en direcciones opuestas.

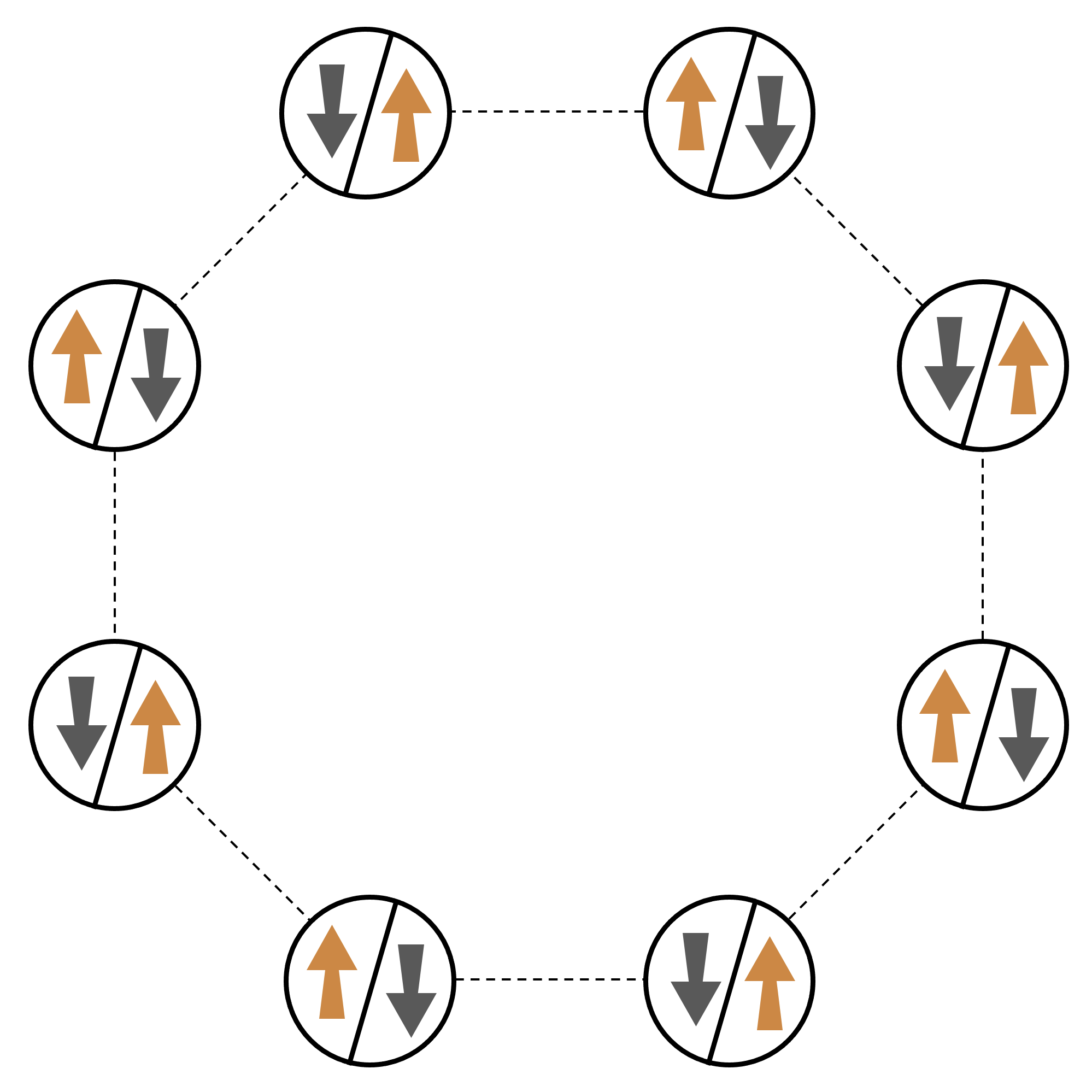
Diagrama que conecta 8 nodos circulares que contienen flechas inversas hacia arriba y hacia abajo.

Arreglo

Usaremos un átomo neutro para representar cada espín, y los estados de espín «arriba» y «abajo» se codificarán en el estado excitado de Rydberg y en el estado fundamental de los átomos, respectivamente. En primer lugar, creamos la disposición bidimensional. Podemos programar el anillo de tiradas anterior con el siguiente código.

Requisitos previos: Es necesario instalar el Braket mediante pip. SDK (Si utiliza una instancia de portátil alojada en Braket, esta SDK viene preinstalada con las computadoras portátiles). Para reproducir los gráficos, también es necesario instalar matplotlib por separado con el comando shell. pip install matplotlib


import numpy as np
   import matplotlib.pyplot as plt  # required for plotting
   
   from braket.ahs.atom_arrangement import AtomArrangement
   
   a = 5.7e-6  # nearest-neighbor separation (in meters)
   
   register = AtomArrangement()
   register.add(np.array([0.5, 0.5 + 1/np.sqrt(2)]) * a)
   register.add(np.array([0.5 + 1/np.sqrt(2), 0.5]) * a)
   register.add(np.array([0.5 + 1/np.sqrt(2), - 0.5]) * a)
   register.add(np.array([0.5, - 0.5 - 1/np.sqrt(2)]) * a)
   register.add(np.array([-0.5, - 0.5 - 1/np.sqrt(2)]) * a)
   register.add(np.array([-0.5 - 1/np.sqrt(2), - 0.5]) * a)
   register.add(np.array([-0.5 - 1/np.sqrt(2), 0.5]) * a)
   register.add(np.array([-0.5, 0.5 + 1/np.sqrt(2)]) * a)

con el que también podemos graficar


fig, ax = plt.subplots(1, 1, figsize=(7,7))
   xs, ys = [register.coordinate_list(dim) for dim in (0, 1)]
   ax.plot(xs, ys, 'r.', ms=15)
   for idx, (x, y) in enumerate(zip(xs, ys)):
       ax.text(x, y, f" {idx}", fontsize=12)
   plt.show()  # this will show the plot below in an ipython or jupyter session

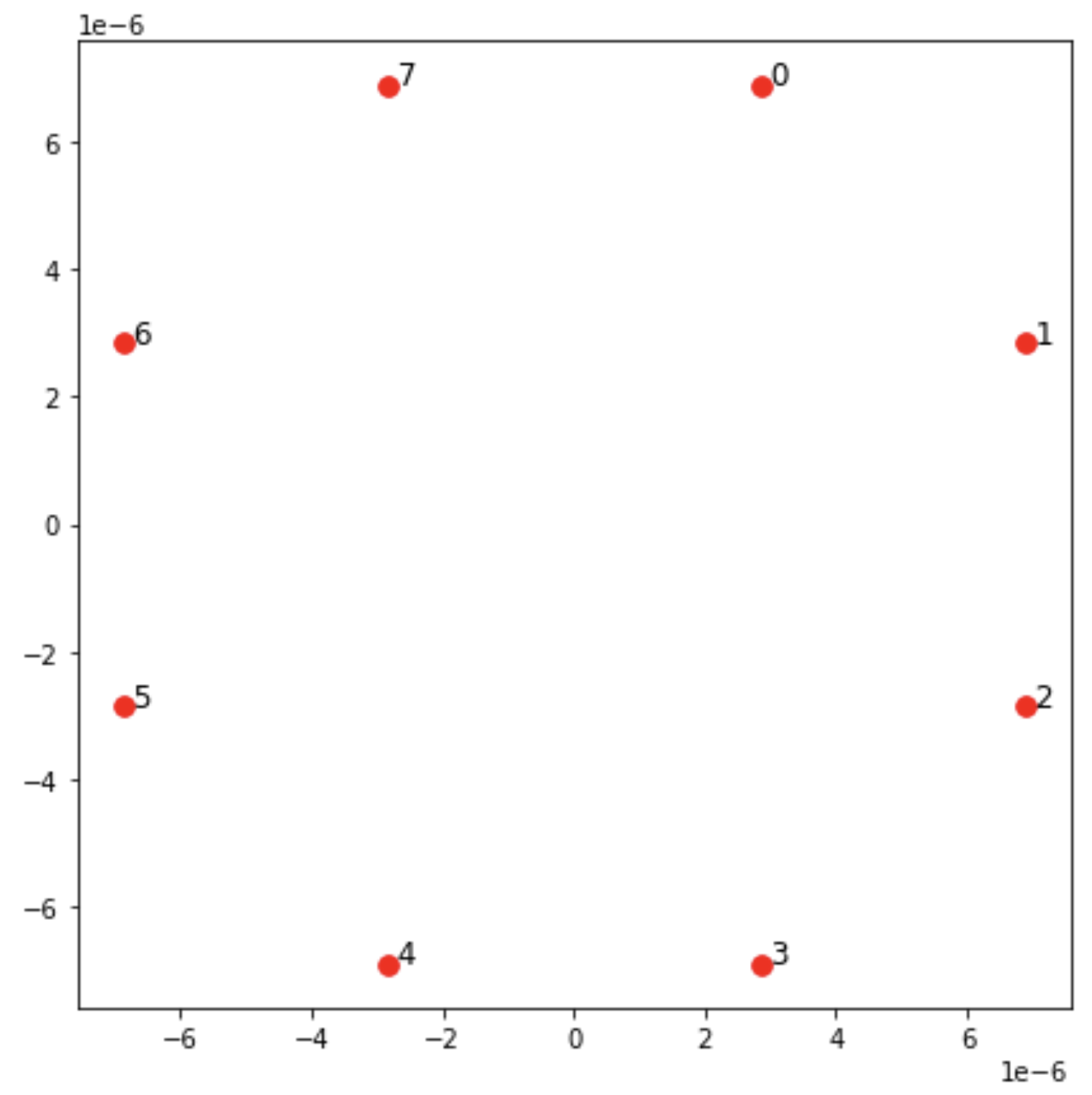
Diagrama de dispersión que muestra los puntos distribuidos entre valores positivos y negativos en ambos ejes.

Interacción

Para preparar la fase antiferromagnética, necesitamos inducir interacciones entre espines vecinos. Para ello utilizamos la interacción de van der Waals, que se implementa de forma nativa mediante dispositivos de átomos neutros (como el Aquila dispositivo de QuEra). Usando la representación del espín, el término hamiltoniano para esta interacción se puede expresar como la suma de todos los pares de espines (j, k).

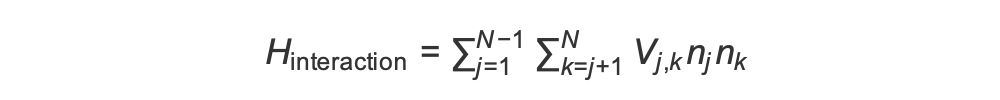
En este caso, nj=↑ _j ～～↑ _j es un operador que toma el valor de 1 solo si el espín j está en el estado «hacia arriba» y 0 en caso contrario. La fuerza es V _j,k =C₆/(d_j,k) ⁶, donde C ₆ es el coeficiente fijo y d es la distancia euclidiana entre los _j,k espines j y k. El efecto inmediato de este término de interacción es que cualquier estado en el que tanto el espín j como el espín k estén «hacia arriba» tiene una energía elevada (en la cantidad V). _j,k Al diseñar cuidadosamente el resto del AHS programa, esta interacción evitará que los giros vecinos estén ambos en estado «positivo», un efecto que se conoce comúnmente como «bloqueo de Rydberg».

Campo de conducción

Al principio del AHS programa, todos los giros (por defecto) comienzan en su estado «inactivo», es decir, se encuentran en la denominada fase ferromagnética. Con la vista puesta en nuestro objetivo de preparar la fase antiferromagnética, especificamos un campo impulsor coherente y dependiente del tiempo que hace que los espines pasen sin problemas de este estado a un estado compuesto por varios cuerpos, en el que se prefieren los estados «ascendentes». El hamiltoniano correspondiente se puede escribir como

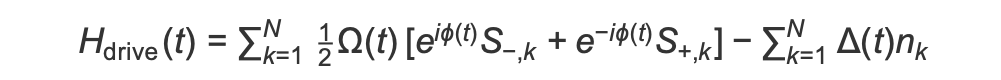
Ecuación matemática que representa el cálculo de una función impulsora hamiltoniana.

donde Ω (t), ω (t) y △ (t) son la amplitud global (también conocida como frecuencia de Rabi), la fase y la desafinación del campo impulsor, que dependen del tiempo y afectan a todos los giros de manera uniforme. En este caso_−,k, S _k =↓ _k ～ ↑ y S _+,k =( S_−,k) ^† =↑ _k ～～ ↓ _k son los operadores de subida y bajada del espín k, respectivamente, y n _k _k =↑ _k ↑ es el mismo operador que antes. La parte Ω del campo conductor acopla de manera coherente los estados «hacia abajo» y «hacia arriba» de todos los giros simultáneamente, mientras que la parte λ controla la recompensa de energía para los estados «hacia arriba».

Para programar una transición suave de la fase ferromagnética a la fase antiferromagnética, especificamos el campo impulsor con el siguiente código.


from braket.timings.time_series import TimeSeries
   from braket.ahs.driving_field import DrivingField
   
   # smooth transition from "down" to "up" state
   time_max = 4e-6  # seconds
   time_ramp = 1e-7  # seconds
   omega_max = 6300000.0  # rad / sec
   delta_start = -5 * omega_max
   delta_end = 5 * omega_max
   
   omega = TimeSeries()
   omega.put(0.0, 0.0)
   omega.put(time_ramp, omega_max)
   omega.put(time_max - time_ramp, omega_max)
   omega.put(time_max, 0.0)
   
   delta = TimeSeries()
   delta.put(0.0, delta_start)
   delta.put(time_ramp, delta_start)
   delta.put(time_max - time_ramp, delta_end)
   delta.put(time_max, delta_end)
   
   phi = TimeSeries().put(0.0, 0.0).put(time_max, 0.0)
   
   drive = DrivingField(
       amplitude=omega,
       phase=phi,
       detuning=delta
   )

Podemos visualizar la serie temporal del campo conductor con el siguiente script.


fig, axes = plt.subplots(3, 1, figsize=(12, 7), sharex=True)
   
   ax = axes[0]
   time_series = drive.amplitude.time_series
   ax.plot(time_series.times(), time_series.values(), '.-');
   ax.grid()
   ax.set_ylabel('Omega [rad/s]')
   
   ax = axes[1]
   time_series = drive.detuning.time_series
   ax.plot(time_series.times(), time_series.values(), '.-');
   ax.grid()
   ax.set_ylabel('Delta [rad/s]')
   
   ax = axes[2]
   time_series = drive.phase.time_series
   # Note: time series of phase is understood as a piecewise constant function
   ax.step(time_series.times(), time_series.values(), '.-', where='post');
   ax.set_ylabel('phi [rad]')
   ax.grid()
   ax.set_xlabel('time [s]')
   
   plt.show()  # this will show the plot below in an ipython or jupyter session

Tres gráficos que muestran phi, delta y omega a lo largo del tiempo. La subgráfica superior muestra el crecimiento justo por encima de los 6 rads/s, donde permanece durante 4 segundos hasta que vuelve a caer a 0. La subgráfica central representa el crecimiento lineal asociado de la derivada, y la subgráfica inferior ilustra una línea plana cercana a cero.

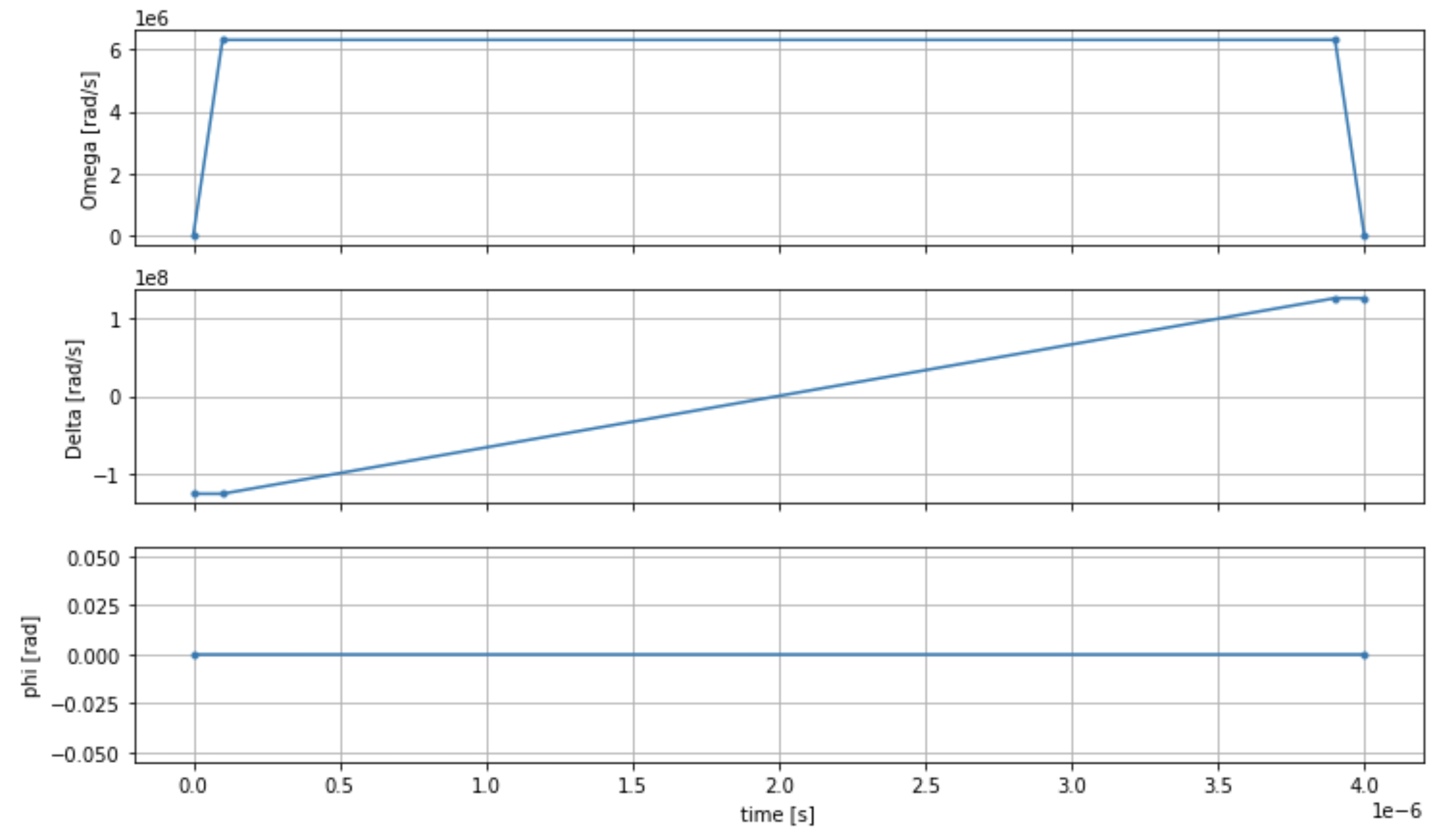
AHSprograma

El registro, el campo conductor (y las interacciones implícitas de van der Waals) componen el programa de simulación hamiltoniana analógica. ahs_program


from braket.ahs.analog_hamiltonian_simulation import AnalogHamiltonianSimulation
   
   ahs_program = AnalogHamiltonianSimulation(
       register=register,
       hamiltonian=drive
   )

Se ejecuta en un simulador local

Como este ejemplo es pequeño (menos de 15 tiradas), antes de ejecutarlo en un AHS -compatibleQPU, podemos ejecutarlo en el AHS simulador local que viene con el Braket. SDK Como el simulador local está disponible de forma gratuita con el BraketSDK, esta es una buena práctica para asegurarnos de que nuestro código se ejecute correctamente.

En este caso, podemos establecer el número de disparos en un valor alto (por ejemplo, 1 millón) porque el simulador local registra la evolución temporal del estado cuántico y extrae muestras del estado final; por lo tanto, aumenta el número de disparos y aumenta el tiempo de ejecución total solo marginalmente.


from braket.devices import LocalSimulator
   device = LocalSimulator("braket_ahs")
   
   result_simulator = device.run(
       ahs_program,
       shots=1_000_000
   ).result()  # takes about 5 seconds

Analizando los resultados del simulador

Podemos sumar los resultados de los tiros con la siguiente función que deduce el estado de cada giro (que puede ser «d» para «abajo», «u» para «arriba» o «e» para un sitio vacío) y cuenta cuántas veces se ha producido cada configuración en los tiros.


from collections import Counter
   
   def get_counts(result):
       """Aggregate state counts from AHS shot results
   
       A count of strings (of length = # of spins) are returned, where
       each character denotes the state of a spin (site):
          e: empty site
          u: up state spin
          d: down state spin
   
       Args:
          result (braket.tasks.analog_hamiltonian_simulation_quantum_task_result.AnalogHamiltonianSimulationQuantumTaskResult)
   
       Returns
           dict: number of times each state configuration is measured
   
       """
       state_counts = Counter()
       states = ['e', 'u', 'd']
       for shot in result.measurements:
           pre = shot.pre_sequence
           post = shot.post_sequence
           state_idx = np.array(pre) * (1 + np.array(post))
           state = "".join(map(lambda s_idx: states[s_idx], state_idx))
           state_counts.update((state,))
       return dict(state_counts)
   
   counts_simulator = get_counts(result_simulator)  # takes about 5 seconds
   print(counts_simulator)


{'udududud': 330944, 'dudududu': 329576, 'dududdud': 38033, ...}

Este counts es un diccionario que cuenta el número de veces que se observa cada configuración de estado en las tomas. También podemos visualizarlos con el siguiente código.


from collections import Counter
   
   def has_neighboring_up_states(state):
       if 'uu' in state:
           return True
       if state[0] == 'u' and state[-1] == 'u':
           return True
       return False
   
   def number_of_up_states(state):
       return Counter(state)['u']
   
   def plot_counts(counts):
       non_blockaded = []
       blockaded = []
       for state, count in counts.items():
           if not has_neighboring_up_states(state):
               collection = non_blockaded
           else:
               collection = blockaded
           collection.append((state, count, number_of_up_states(state)))
   
       blockaded.sort(key=lambda _: _[1], reverse=True)
       non_blockaded.sort(key=lambda _: _[1], reverse=True)
   
       for configurations, name in zip((non_blockaded,
                                       blockaded),
                                       ('no neighboring "up" states',
                                       'some neighboring "up" states')):
           plt.figure(figsize=(14, 3))
           plt.bar(range(len(configurations)), [item[1] for item in configurations])
           plt.xticks(range(len(configurations)))
           plt.gca().set_xticklabels([item[0] for item in configurations], rotation=90)
           plt.ylabel('shots')
           plt.grid(axis='y')
           plt.title(f'{name} configurations')
           plt.show()
   
   plot_counts(counts_simulator)

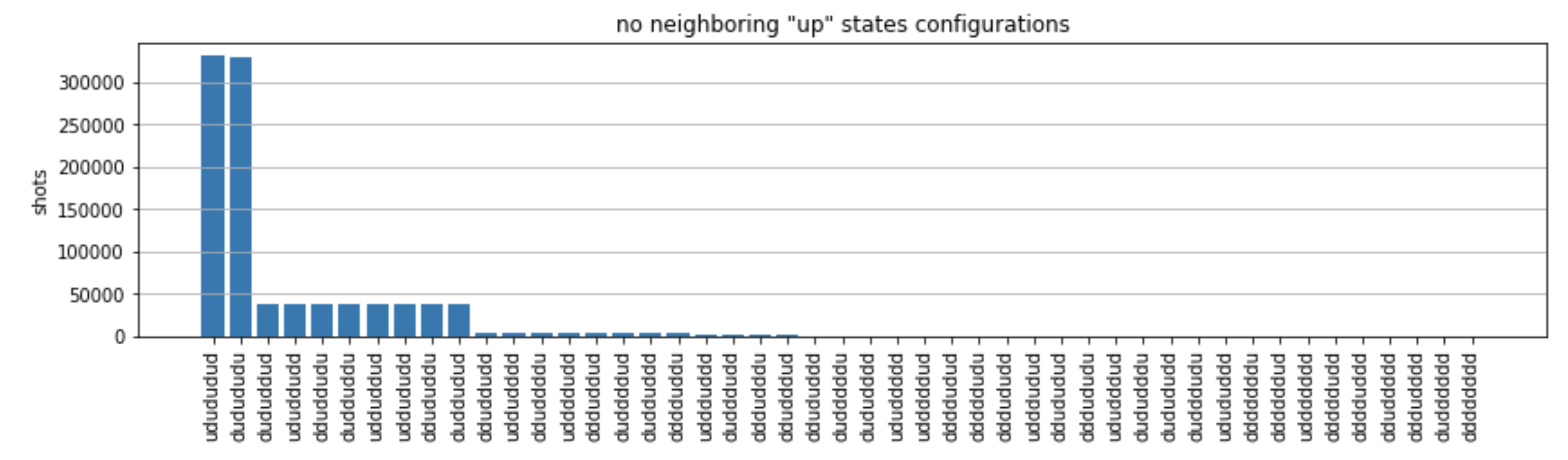
Gráfico de barras que muestra un gran número de tomas sin configuraciones de estados «ascendentes» adyacentes.

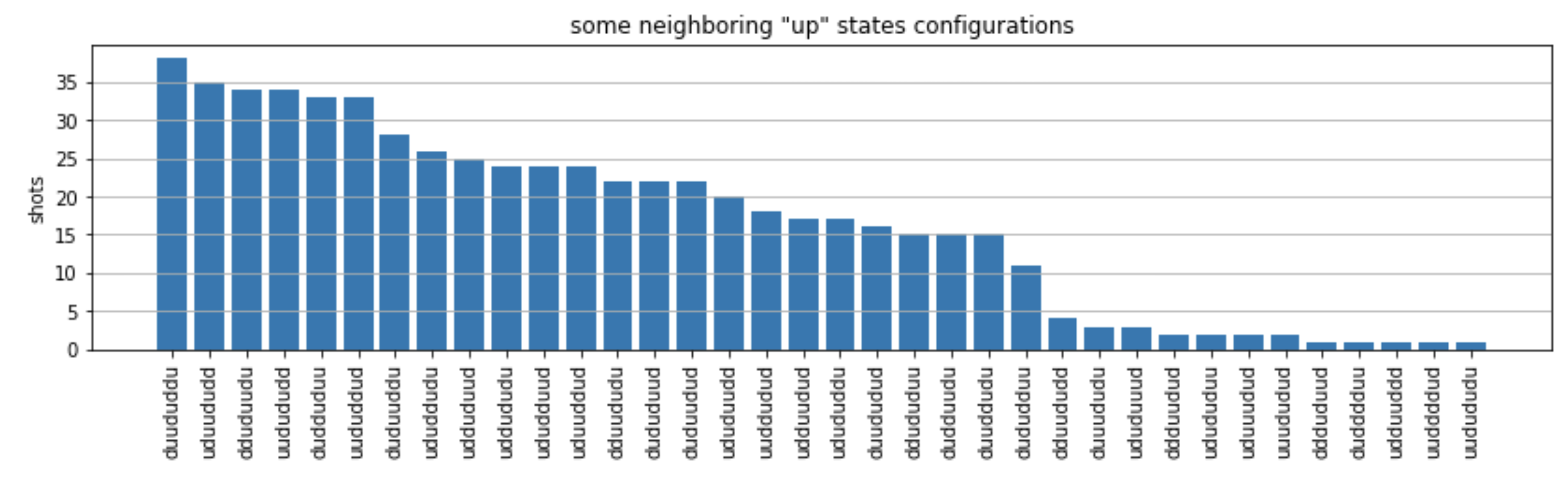
Gráfico de barras que muestra imágenes de algunas configuraciones de estados «ascendentes» vecinas, con estados que descienden de valores altos a valores bajos.

A partir de los gráficos, podemos leer las siguientes observaciones para comprobar que hemos preparado con éxito la fase antiferromagnética.

En general, los estados no bloqueados (en los que no hay dos espines vecinos que estén en el estado «hacia arriba») son más comunes que los estados en los que al menos un par de espines vecinos se encuentran ambos en estados «hacia arriba».
En general, se prefieren los estados con más excitaciones «ascendentes», a menos que la configuración esté bloqueada.
Los estados más comunes son, de hecho, los estados antiferromagnéticos perfectos y. "dudududu" "udududud"
Los segundos estados más comunes son aquellos en los que solo hay 3 excitaciones «ascendentes» con separaciones consecutivas de 1, 2, 2. Esto demuestra que la interacción de van der Waals también tiene un efecto (aunque mucho menor) en los vecinos más cercanos.

Corre Aquila QuEra QPU

Requisitos previos: Además de instalar el Braket SDK, si eres nuevo en Amazon Braket, asegúrate de haber completado los pasos necesarios para empezar.

nota

Si utiliza una instancia de portátil alojada en Braket, la instancia viene preinstalada con la instancia. SDK

Con todas las dependencias instaladas, podemos conectarnos al Aquila QPU.


from braket.aws import AwsDevice
   
   aquila_qpu = AwsDevice("arn:aws:braket:us-east-1::device/qpu/quera/Aquila")

Para que nuestro AHS programa sea adecuado para QuEra máquina, necesitamos redondear todos los valores para cumplir con los niveles de precisión permitidos por la Aquila QPU. (Estos requisitos se rigen por los parámetros del dispositivo que llevan la palabra «Resolución» en su nombre. Los podemos ver ejecutándolos aquila_qpu.properties.dict() en un cuaderno. Para obtener más detalles sobre las capacidades y los requisitos de Aquila, consulte la introducción al cuaderno Aquila.) Podemos hacerlo llamando al método. discretize


discretized_ahs_program = ahs_program.discretize(aquila_qpu)

Ahora podemos ejecutar el programa (por ahora solo se ejecutan 100 disparos) en el Aquila QPU.

nota

Ejecutando este programa en el Aquila el procesador conllevará un coste. Amazon Braket SDK incluye un rastreador de costos que permite a los clientes establecer límites de costos y realizar un seguimiento de sus costos casi en tiempo real.


task = aquila_qpu.run(discretized_ahs_program, shots=100)
   
   metadata = task.metadata()
   task_arn = metadata['quantumTaskArn']
   task_status = metadata['status']
   
   print(f"ARN: {task_arn}")
   print(f"status: {task_status}")


task ARN: arn:aws:braket:us-east-1:123456789012:quantum-task/12345678-90ab-cdef-1234-567890abcdef
   task status: CREATED

Debido a la gran variación del tiempo que puede tardar en ejecutarse una tarea cuántica (según los intervalos de QPU disponibilidad y el uso), es una buena idea anotar la tarea ARN cuántica para poder comprobar su estado más adelante con el siguiente fragmento de código.


# Optionally, in a new python session
   
   from braket.aws import AwsQuantumTask
   
   SAVED_TASK_ARN = "arn:aws:braket:us-east-1:123456789012:quantum-task/12345678-90ab-cdef-1234-567890abcdef"
   
   task = AwsQuantumTask(arn=SAVED_TASK_ARN)
   metadata = task.metadata()
   task_arn = metadata['quantumTaskArn']
   task_status = metadata['status']
   
   print(f"ARN: {task_arn}")
   print(f"status: {task_status}")


*[Output]*
   task ARN: arn:aws:braket:us-east-1:123456789012:quantum-task/12345678-90ab-cdef-1234-567890abcdef
   task status: COMPLETED

Una vez que el estado esté COMPLETED (que también se puede comprobar desde la página de tareas cuánticas de la consola Amazon Braket), podemos consultar los resultados con:


result_aquila = task.result()

Analizando los resultados QPU

Usando las mismas get_counts funciones que antes, podemos calcular los recuentos:


counts_aquila = get_counts(result_aquila)
   print(counts_aquila)


*[Output]*
   {'udududud': 24, 'dudududu': 17, 'dududdud': 3, ...}

y graficarlos conplot_counts:


plot_counts(counts_aquila)

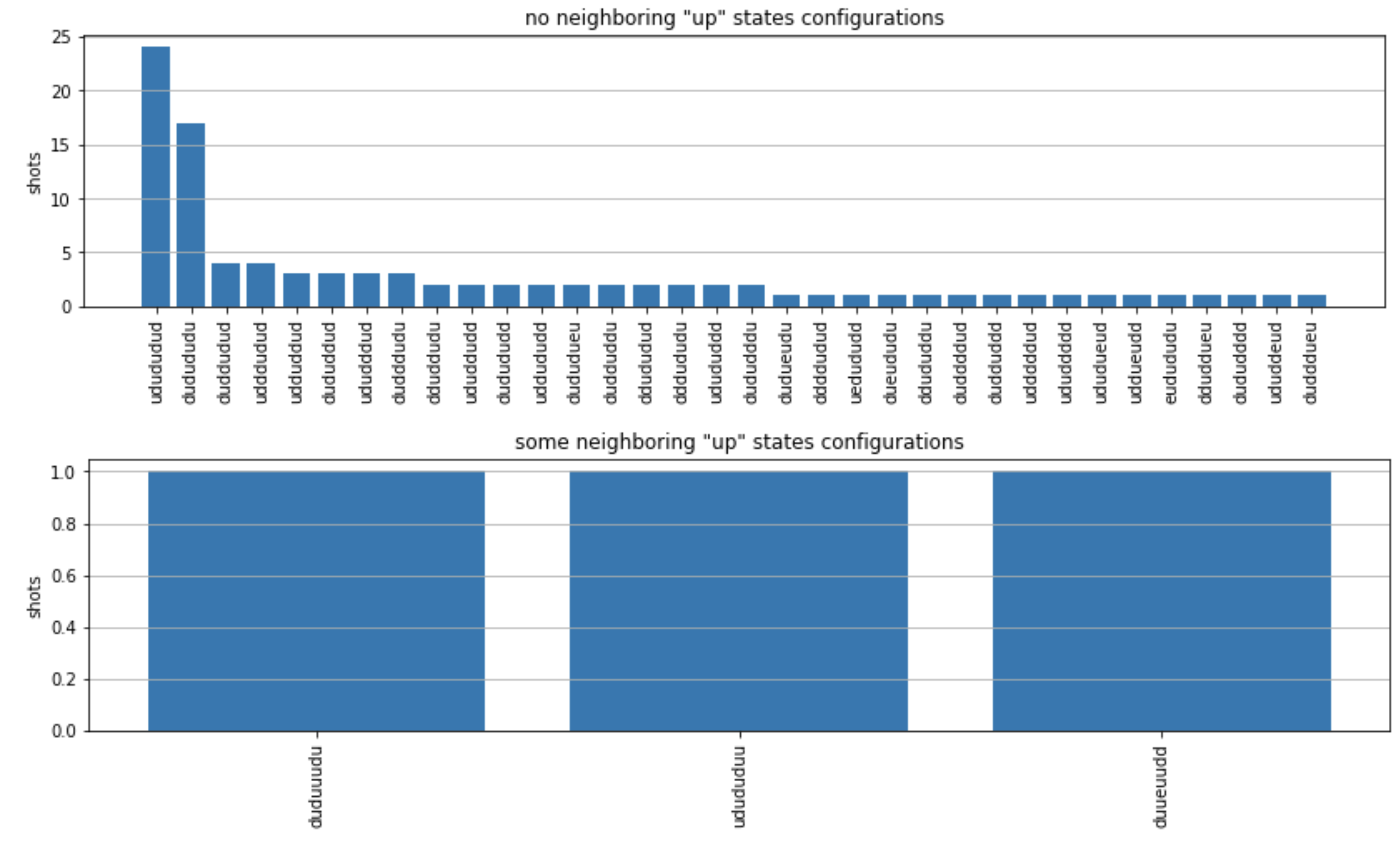
Gráfico de barras que muestra la tasa de disparos con y sin estados «positivos» contiguos.

Tenga en cuenta que una pequeña fracción de las tomas tiene sitios vacíos (marcados con una «e»). Esto se debe a una imperfección del 1 al 2% por átomo en la preparación del Aquila QPU. Además, los resultados coinciden con la simulación dentro de la fluctuación estadística esperada debido al reducido número de disparos.

Siguientes pasos

Enhorabuena, ya ha ejecutado su primera AHS carga de trabajo en Amazon Braket con el AHS simulador local y el Aquila QPU.

Para obtener más información sobre la física de Rydberg, la simulación hamiltoniana analógica y la Aquila dispositivo, consulte nuestros ejemplos de cuadernos.

Aviso JavaScript está desactivado o no está disponible en su navegador.

Para utilizar la documentación de AWS, debe estar habilitado JavaScript. Para obtener más información, consulte las páginas de ayuda de su navegador.

Convenciones del documento

Simulación hamiltoniana analógica (avanzada)

Envíe un programa analógico utilizando QuEra Aquila