Paso 4: Evaluar los predictores

Un flujo de trabajo típico en el machine learning consiste en entrenar un conjunto de modelos o combinaciones de modelos en un conjunto de entrenamiento y evaluar su precisión en un conjunto de datos de retención. En esta sección se explica cómo dividir los datos históricos y qué métricas se deben utilizar para evaluar los modelos en la previsión de series temporales. En el ámbito de las previsiones, la técnica de backtesting es la principal herramienta para evaluar su precisión.

Backtesting

Un marco adecuado de evaluación y backtesting es uno de los factores más importantes para convertir una aplicación de machine learning en un éxito. Si consigue realizar un backtesting satisfactorio con sus modelos, podrá aumentar la confianza en su poder predictivo futuro. Además, puede ajustar los modelos mediante la optimización de hiperparámetros (HPO), aprender combinaciones de modelos y habilitar el metaaprendizaje y el AutoML.

El tiempo característico de la predicción de series temporales hace que sea diferente, en términos de metodología de evaluación y backtesting, de otros campos del machine learning aplicado. Por lo general, en las tareas de machine learning, para evaluar el error predictivo en una prueba de backtest, se divide un conjunto de datos por elementos. Por ejemplo, para la validación cruzada en tareas relacionadas con imágenes, se entrena el modelo con cierto porcentaje de las imágenes y, a continuación, se utilizan otras partes para realizar pruebas y validar. En la previsión, hay que dividir principalmente por tiempo (y, en menor medida, por elementos) para garantizar que no se filtre información del conjunto de entrenamiento al conjunto de prueba o validación y que se simule el caso de producción lo más fielmente posible.

La división por tiempo debe hacerse con cuidado, ya que no conviene elegir un solo punto en el tiempo, sino varios. De lo contrario, la precisión dependería demasiado de la fecha de inicio de la previsión, tal como se define en el punto de división. Una evaluación continua de las previsiones, en la que se realizan una serie de divisiones en varios puntos temporales y se obtiene el resultado promedio, genera resultados más sólidos y fiables en el backtest. En la siguiente figura se ilustran cuatro divisiones diferentes del backtest.

Ilustración de cuatro escenarios diferentes de backtesting con un tamaño creciente del conjunto de entrenamiento, pero un tamaño constante de las pruebas

En la figura anterior, todos los escenarios de backtesting tienen datos disponibles en su totalidad para poder evaluar los valores previstos con respecto a los reales.

La razón por la que se necesitan varias ventanas de backtesting es que la mayoría de las series temporales del mundo real normalmente no son estacionarias. La empresa de comercio electrónico del caso práctico tiene su sede en Norteamérica y gran parte de su demanda de productos se acentúa en la temporada alta del cuarto trimestre, con picos de demanda específicos en torno al Día de Acción de Gracias y antes de Navidad. En la temporada de compras del cuarto trimestre, la variabilidad de las series temporales es mayor que durante el resto del año. Al disponer de varias ventanas de backtesting, es posible evaluar los modelos de previsión en un entorno más equilibrado.

Para cada escenario de backtesting, la siguiente figura muestra los elementos básicos de la terminología de Amazon Forecast. Amazon Forecast divide automáticamente los datos en los conjuntos de datos de entrenamiento y de prueba. Amazon Forecast decide cómo dividir los datos de entrada mediante el parámetro BackTestWindowOffset especificado como parámetro en la API create_predictor o con su valor predeterminado de ForecastHorizon.

En la siguiente figura puede ver el primer caso, más habitual, en el que los parámetros ForecastHorizon y BackTestWindowOffset no son iguales. El parámetro BackTestWindowOffset define una fecha de inicio de previsión virtual, que aparece como línea vertical discontinua en la siguiente figura. Se puede utilizar para responder a la siguiente pregunta hipotética: si el modelo se implementa ese día, ¿cuál sería la previsión? El parámetro ForecastHorizon define el número de pasos de tiempo que se deben predecir desde la fecha de inicio de la previsión virtual.

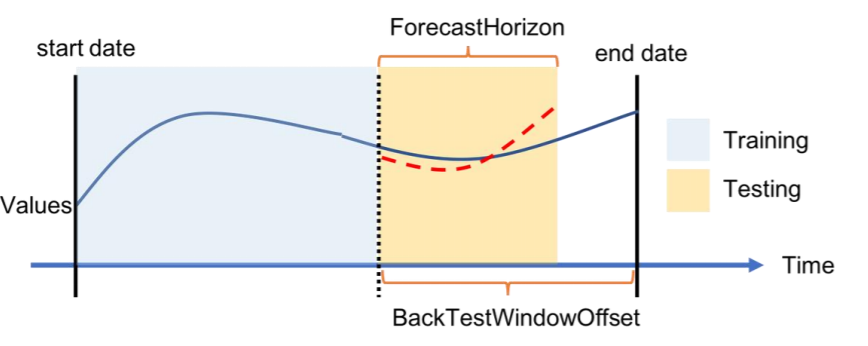
Ilustración de un único escenario de backtesting y su configuración en Amazon Forecast

Amazon Forecast puede exportar los valores previstos y las métricas de precisión generadas durante el backtesting. Los datos exportados se pueden utilizar para evaluar determinados elementos en puntos de tiempo y cuantiles específicos.

Cuantiles de predicción y métricas de precisión

Los cuantiles de predicción pueden proporcionar un límite superior e inferior para las previsiones. Por ejemplo, el uso de los tipos de previsión 0,1 (P10), 0,5 (P50) y 0,9 (P90) proporciona un rango de valores que se determina intervalo de confianza del 80 % en torno a la previsión del P50. Al generar predicciones en los cuantiles P10, P50 y P90, cabe esperar que el valor real se sitúe entre esos límites el 80 % de las veces.

En este documento se analizan con más detalle los cuantiles en el paso 5.

Amazon Forecast utiliza las métricas de precisión de pérdida cuantil ponderada (wQL), raíz del error cuadrático medio (RMSE) y error porcentual absoluto ponderado (WAPE) para evaluar los predictores durante las pruebas de backtesting.

Pérdida cuantil ponderada (wQL)

La métrica de error de pérdida cuantil ponderada (wQL) mide la precisión de la previsión de un modelo en un cuantil específico. Resulta particularmente útil cuando la predicción excesiva y la predicción insuficiente suponen costes diferentes. Al establecer la ponderación (τ) de la función wQL se incorporan automáticamente diferentes penalizaciones por quedarse corto o pasarse en la predicción.

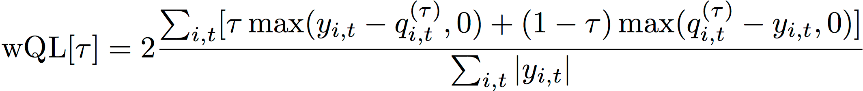
Función wQL

Donde:

• τ: un cuantil del conjunto {0,01, 0,02, ..., 0,99}

• qi,t(τ): el cuantil τ que predice el modelo.

• yi,t: el valor observado en el punto (i,t)

Error porcentual absoluto ponderado (WAPE)

El error porcentual absoluto ponderado (WAPE) es una métrica que se usa habitualmente para medir la precisión del modelo. Mide la desviación general de los valores previstos con respecto a los valores observados.

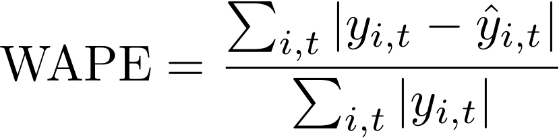
WAPE

Donde:

• yi,t: el valor observado en el punto (i,t)

• ŷi,t: el valor previsto en el punto (i,t)

La previsión utiliza la previsión media como valor predicho, ŷi,t.

Raíz del error cuadrático medio (RMSE)

La raíz del error cuadrático medio (RMSE) es una métrica que se usa habitualmente para medir la precisión del modelo. Al igual que el WAPE, mide la desviación general de las estimaciones con respecto a los valores observados.

Donde:

• yi,t: el valor observado en el punto (i,t)

• ŷi,t: el valor previsto en el punto (i,t)

• nT: el número de puntos de datos en un conjunto de pruebas

La previsión utiliza la previsión media como valor predicho, ŷi,t. Al calcular las métricas predictoras, nT es el número de puntos de datos en una ventana de backtesting.

Problemas con WAPE y RMSE

En la mayoría de los casos, las previsiones puntuales que se pueden generar internamente o a partir de otras herramientas de previsión deben coincidir con las previsiones medias o del cuantil p50. Tanto para WAPE como para RMSE, Amazon Forecast utiliza la previsión media para representar el valor previsto (yhat).

Para una tau = 0,5 en la ecuación de wQL[tau], ambas ponderaciones son iguales y el wQL[0,5] se reduce al error porcentual absoluto ponderado (WAPE) que se utiliza comúnmente para las previsiones puntuales:

donde yhat = q(0,5) es la previsión informática. Se utiliza un factor de escala de 2 en la fórmula de wQL para cancelar el factor de 0,5 y obtener la expresión del WAPE[mediana] exacta.

Tenga en cuenta que la definición anterior del WAPE difiere de una interpretación común del error porcentual absoluto medio (MAPE). La diferencia está en el denominador. La forma en que se define el WAPE arriba evita el problema de la división por 0, un problema que ocurre con frecuencia en escenarios del mundo real, como la empresa de comercio electrónico del caso práctico, que suele vender 0 unidades de una SKU determinada en un día determinado.

A diferencia de la métrica de pérdida cuantil ponderada para tau no igual a 0,5, el sesgo inherente a cada cuantil no se puede captar mediante un cálculo como el WAPE, en el que las ponderaciones son iguales. Otras desventajas del WAPE incluyen que no es simétrico, tiene una inflación excesiva de los errores porcentuales para números pequeños y es solo una métrica puntual.

La RMSE es el cuadrado del término de error en el WAPE y una métrica de error común en otras aplicaciones de aprendizaje automático. La métrica RMSE funciona mejor en modelos en los que los errores individuales tienen una magnitud uniforme, ya que una variación grande en los errores aumentará la RMSE de forma desproporcionada. Debido al error cuadrático, unos cuantos valores mal previstos en una buena previsión pueden aumentar el RMSE. Además, como consecuencia de la elevación al cuadrado de los términos, los términos de error más pequeños tienen menos peso en la RMSE que en el WAPE.

Las métricas de precisión permiten una evaluación cuantitativa de las previsiones. En particular, para las comparaciones a gran escala (por ejemplo, si el método A es mejor que el método B en general), resultan cruciales. Sin embargo, a menudo es importante complementar esto con elementos visuales para cada SKU.