Les traductions sont fournies par des outils de traduction automatique. En cas de conflit entre le contenu d'une traduction et celui de la version originale en anglais, la version anglaise prévaudra.
Décomposer l'incertitude
Les réseaux neuronaux bayésiens (BNNs) produisent une distribution prédictive
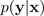, qui fournit un ensemble de prédictions différentes à partir desquelles vous pouvez estimer la variance,
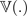c'est-à-dire l'incertitude prédictive totale.
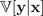L'incertitude prédictive totale peut être divisée en deux composantes d'incertitude en utilisant la loi de la variance totale :
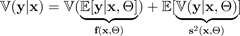
La valeur attendue
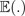d'une variable cible
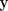, compte tenu des paramètres d'entrée
et aléatoires
qui spécifient un BNN
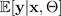, est estimée par un BNN avec une seule propagation vers l'avant et désignée par.
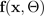La variance de la cible, compte tenu des paramètres d'entrée et aléatoires
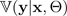, est également émise par le BNN et désignée par.
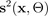Ainsi, l'incertitude prédictive totale est la somme de ces deux nombres :
-
La variance par rapport aux moyennes prédites du BNN
— l'incertitude épistémique -
La moyenne de la variance prédite du BNN
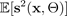— l'incertitude aléatoire
La formule suivante montre comment calculer l'incertitude totale conformément à (Kendall et Gal 2017). BNNs entrez
, générez une configuration
de paramètres aléatoire et effectuez une seule propagation vers l'avant à travers le réseau neuronal pour obtenir une moyenne
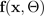et une variance
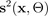. Nous désignons une génération aléatoire, ou simulation, par ~. Avec fixed
, vous pouvez répéter ce processus
plusieurs fois pour obtenir un ensemble :
Ces
nombreux échantillons
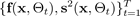fournissent les statistiques nécessaires pour déterminer les incertitudes. Pour ce faire, vous pouvez estimer l'incertitude épistémique et l'incertitude aléatoire séparément, puis en faisant leur somme, comme indiqué précédemment dans la première équation de cette section.
