Fonctionnement de l'algorithme PCA - Amazon SageMaker
Mode 1 : RegularMode 2 : Randomized

Les traductions sont fournies par des outils de traduction automatique. En cas de conflit entre le contenu d'une traduction et celui de la version originale en anglais, la version anglaise prévaudra.

Fonctionnement de l'algorithme PCA

PCA (Principal Component Analysis) est un algorithme d'apprentissage qui diminue la dimensionnalité (nombre de fonctions) au sein d'un ensemble de données tout en conservant autant d'informations que possible.

L'algorithme PCA réduit la dimensionnalité en recherchant un nouvel ensemble de variables appelées composantes et qui sont constituées de caractéristiques originales, mais décorrélées les unes des autres. Le premier composant représente la plus grande variabilité possible dans les données, le deuxième composant la deuxième variabilité la plus importante, et ainsi de suite.

Il s'agit d'un algorithme de réduction de dimensionnalité sans surveillance. Dans l'apprentissage non supervisé, les étiquettes qui pourraient être associées à des objets de l'ensemble de données d'entraînement ne sont pas utilisées.

Soit en entrée une matrice avec les lignes 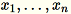x_1,…,x_n chacune de dimension 1 * d, les données sont partitionnées en mini-lots de lignes et distribuées entre les nœuds d'apprentissage (travaux). Chaque worker calcule ensuite un résumé de ses données. Les résumés des différents workers sont ensuite unifiés en une seule solution à la fin du calcul.

Modes

L'algorithme PCA Amazon SageMaker utilise l'un ou l'autre des deux modes pour calculer les résumés, en fonction de la situation :

  • regular : pour les ensembles de données avec données fragmentées et un nombre modéré d'observations et de caractéristiques.

  • randomized : pour les ensembles de données avec un grand nombre d'observations et de caractéristiques. Ce mode utilise un algorithme d'approximation.

Lors de sa dernière étape, l'algorithme effectue la décomposition en valeurs singulières de la solution unifiée, à partir de laquelle les principaux composants sont ensuite dérivés.

Mode 1 : Regular

Les agents de travail calculent 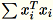\sum x_i^T x_i et \sum x_i .

Note

Comme 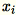x_i sont 1 * d des vecteurs de ligne, x_i^T x_i est une matrice (non un scalaire). L'utilisation des vecteurs de ligne au sein du code nous permet d'obtenir une mise en cache efficace.

La matrice de covariance est calculée comme 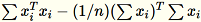\sum x_i^T x_i - (1/n) (\sum x_i)^T \sum x_i et ses principaux vecteurs num_components forment le modèle.

Note

Si subtract_mean a la valeur False, nous évitons de calculer et de soustraire \sum x_i .

Utilisez cet algorithme lorsque la dimension d des vecteurs est suffisamment petite pour que 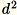d^2 puisse contenir en mémoire.

Mode 2 : Randomized

Lorsque le nombre de fonctions de l'ensemble de données en entrée est de grande taille, nous utilisons une méthode pour estimer approximativement la métrique de covariance. Pour chaque mini-lot 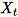X_t de dimension b * d, nous initialisons de façon aléatoire une matrice (num_components + extra_components) * b que nous multiplions par chaque mini-lot, afin de créer une matrice (num_components + extra_components) * d. La somme de ces matrices est calculée par les workers et les serveurs exécutent SVD sur la matrice (num_components + extra_components) * d finale. Les vecteurs num_components singuliers en haut à droite représentent l'approximation des vecteurs singuliers supérieurs de la matrice d'entrée.

\ell = num_components + extra_components. Soit un mini-lot 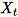X_t de dimension b * d, le travail trace une matrice aléatoire 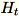H_t de dimension \ell * b . Selon que l'environnement utilise un GPU ou une UC et la taille de la dimension, la matrice est une matrice de signe aléatoire où chaque entrée est +-1 ou une transformation FJLT (Fast Johnson Lindenstrauss Transform ; pour plus d'informations, consultez FJLT Transforms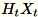 et les articles afférents). Le travail calcule ensuite H_t X_t et maintient 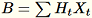B = \sum H_t X_t . 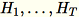Le travail maintient aussi h^T , la somme des colonnes de H_1,..,H_T (T étant le nombre total de mini-lots), et s, la somme de toutes les lignes en entrée. Après le traitement de la totalité de la partition de données, le worker envoie au serveur B, h, s et n (nombre de lignes en entrée).

Indiquez les différentes entrées au serveur comme B^1, h^1, s^1, n^1,… Le serveur calcule B, h, s, n les sommes des entrées respectives. Puis, il calcule 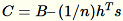C = B – (1/n) h^T s et recherche sa décomposition en valeurs singulières. Les vecteurs singuliers en haut à droite et les valeurs singulières de C sont utilisés comme solution approximative au problème.