Fonctionnement de l'algorithme RCF

Amazon SageMaker Random Cut Forest (RCF) est un algorithme non supervisé permettant de détecter des points de données anormaux au sein d'un ensemble de données. Il s'agit d'observations qui s'écartent de données autrement bien structurées ou calquées. Des anomalies peuvent se manifester sous la forme de pics inattendus au sein de données en séries chronologiques, de ruptures de la périodicité ou de points de données inclassables. Elles sont faciles à décrire, car lorsqu'elles sont affichées dans un tracé, elles sont souvent aisément décelables au milieu des données « normales ». L'inclusion de ces anomalies dans un ensemble de données peut considérablement augmenter la complexité de la tâche de machine learning, car les données « normales » peuvent souvent être décrites à l'aide d'un modèle simple.

L'idée principale derrière l'algorithme RCF consiste à créer une forêt d'arbres où chaque arbre est obtenu à l'aide d'une partition d'un échantillon des données d'entraînement. Par exemple, un échantillon aléatoire des données d'entrée est d'abord déterminé. Cet échantillon aléatoire est ensuite partitionné en fonction du nombre d'arbres de la forêt. Chaque arbre reçoit une partition et organise ce sous-ensemble de points en arbre k-d. La valeur d'anomalie attribuée à un point de données par l'arbre est définie comme le changement prévu de complexité de l'arbre suite à l'ajout de ce point à l'arbre. Par approximation, ceci est inversement proportionnel à la profondeur résultante du point dans l'arbre. L'algorithme Random Cut Forest attribue une valeur d'anomalie en calculant la valeur moyenne de chaque arbre constitutif et en dimensionnant le résultat par rapport à la taille de l'échantillon. L'algorithme RCF est basé sur celui décrit dans la référence bibliographique [1].

Échantillonnage aléatoire des données

La première étape de l'algorithme RCF consiste à obtenir un échantillon aléatoire des données d'entraînement. En particulier, supposons que nous voulions un échantillon de taille 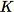à partir du nombre total de points de données. Si les données d'entraînement sont suffisamment petites, il est possible d'utiliser la totalité de l'ensemble de données et de tracer de façon aléatoire 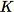éléments de cet ensemble. Cependant, les données d'entraînement sont souvent trop volumineuses pour être toutes utilisées à la fois, et cette approche n'est pas possible. Au lieu de cela, nous utilisons une technique appelée échantillonnage par réservoir.

L'échantillonnage par réservoir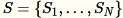 est un algorithme qui permet d'extraire efficacement des échantillons aléatoires à partir d'un ensemble de données dont les éléments ne peuvent être observés qu'individuellement ou par lots. En fait, l'échantillonnage par réservoir fonctionne même lorsque n'est pas connu a priori. Si un seul exemple est demandé, par exemple lorsque 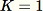, l'algorithme se présente sous la forme suivante :

Algorithme : échantillonnage par réservoir

• Entrée : ensemble ou flux de données

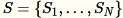
• Initialisez l'échantillon aléatoire

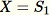
• Pour chaque échantillon observé  :

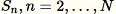  • Choisissez un nombre aléatoire uniforme

  • Si

    • Définir

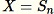
• Return

Cet algorithme sélectionne un échantillon aléatoire de telle sorte que 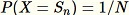pour tous les 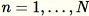. Si 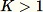, l'algorithme est plus complexe. En outre, il convient de faire la distinction entre l'échantillonnage aléatoire avec et sans remplacement. RCF effectue un échantillonnage par réservoir augmenté sans remplacement sur les données d'entraînement basées sur les algorithmes décrits dans la référence bibliographique [2].

Entraîner un modèle RCF et produire les inférences

L'étape suivante dans RCF est de créer une forêt aléatoire à l'aide de l'échantillon aléatoire de données. Tout d'abord, l'échantillon est partitionné en un certain nombre de partitions de taille égale qui équivaut au nombre d'arbres de la forêt. Ensuite, chaque partition est envoyée à un arbre spécifique. L'arbre organise de manière récursive sa partition selon une arborescence binaire en partitionnant le domaine de données dans des cadres de délimitation.

Il est plus facile d'illustrer cette procédure par un exemple. Supposons qu'un arbre reçoit les ensembles de données bidimensionnels suivants. L'arbre correspondant est initialisé en fonction du nœud racine :

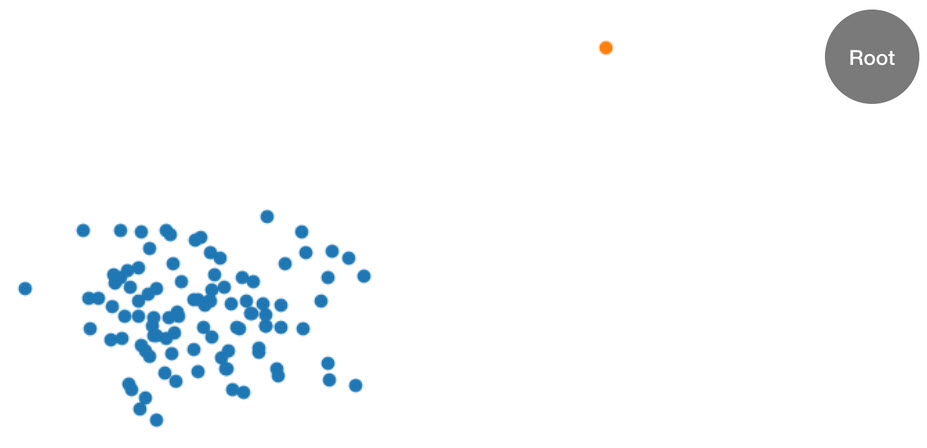
Ensemble de données bidimensionnelles dans lequel la majorité des données se trouve dans un cluster (bleu), à l'exception d'un point de données anormal (orange). L'arbre est initialisé avec un nœud racine.

L'algorithme RCF organise ces données en arbre en commençant par calculer un cadre de délimitation des données, en sélectionnant une dimension aléatoire (en privilégiant les dimensions avec les meilleures « variance »), puis en déterminant de façon aléatoire la position d'une « coupe » hyperplane au travers de cette dimension. Les deux sous-espaces produits définissent leur propre sous-arborescence. Dans cet exemple, la coupe se produit pour séparer un point solitaire du reste de l'échantillon. Le premier niveau de l'arborescence binaire produite se compose de deux nœuds : un entraîné d'une sous-arborescence de points à gauche de la coupe initiale et l'autre qui représente le point unique sur la droite.

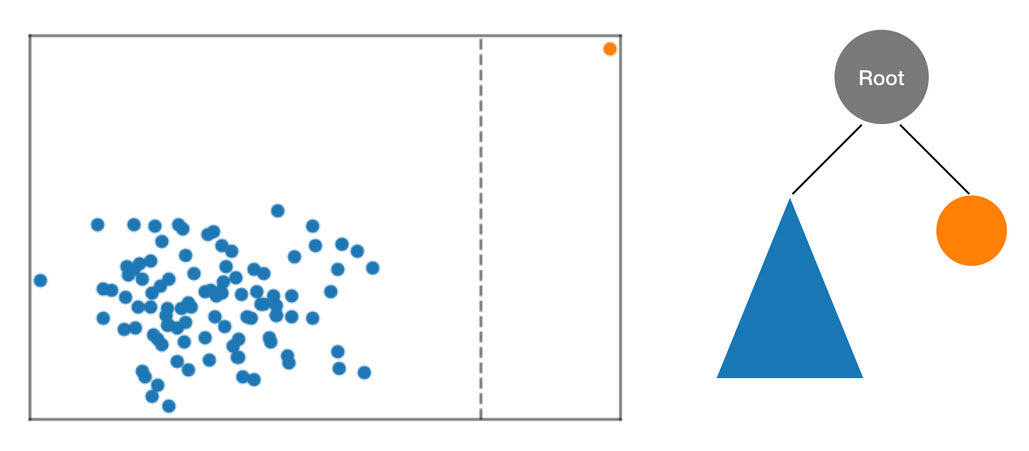
Coupe aléatoire de partitionnement de l'ensemble de données bidimensionnel. Un point de données anormal est plus susceptible de rester isolé dans un cadre de délimitation à une profondeur d'arborescence moindre que celle d'autres points.

Les cadres de limitation sont ensuite calculés pour les moitiés droite et gauche des données, et le processus se répète jusqu'à ce que chaque feuille de l'arbre représente un seul point de données de l'échantillon. Notez que si le point isolé est assez loin, il est plus probable qu'une coupe aléatoire entraîne son isolement. D'après cette observation, on peut conclure que la profondeur de l'arbre est en quelque sorte inversement proportionnelle à la valeur de l'anomalie.

Lorsque vous procédez à l'inférence avec un modèle RCF entraîné, la valeur d'anomalie finale représente la moyenne des valeurs signalées pour chaque arbre. Notez qu'il arrive souvent que le nouveau point de données ne se trouve pas dans l'arbre. Pour déterminer la valeur associée au nouveau point, le point de données est insérée dans l'arbre donné et cet arbre est réassemblé de manière efficace (et temporaire) comme lors du procédé d'entraînement décrit ci-dessus. En d'autres termes, dans l'arbre produit, c'est comme si le point de données d'entrée était un membre de l'échantillon utilisé pour la construction initiale de l'arbre. La valeur signalée est inversement proportionnelle à la profondeur du point d'entrée dans l'arbre.

Choix des hyperparamètres

Les hyperparamètres principaux utilisés pour ajuster le modèle RCF sont num_trees et num_samples_per_tree. L'augmentation de num_trees a pour effet de réduire le bruit observé dans les valeurs d'anomalies, car la valeur finale correspond à la moyenne des valeurs signalées pour chaque arbre. Même si la valeur optimale dépend de l'application, nous vous recommandons de commencer avec 100 arbres pour équilibrer le bruit des valeurs et la complexité du modèle. Notez que la durée de l'inférence est proportionnelle au nombre d'arbres. Bien que la durée de l'entraînement soit également affectée, elle est dominée par l'algorithme d'échantillonnage par réservoir décrit ci-dessus.

Le paramètre num_samples_per_tree est liée à la densité attendue des anomalies dans l'ensemble de données. En particulier, num_samples_per_tree doit être choisi de manière à ce que 1/num_samples_per_tree approche le ratio des données anormales sur les données normales. Par exemple, si 256 échantillons sont utilisés dans chaque arbre, nos données devraient contenir des anomalies 1/256 ou environ 0,4 % du temps. Là encore, la valeur optimale pour cet hyperparamètre dépend de l'application.

Références

1. Sudipto Guha, Nina Mishra, Gourav Roy et Okke Schrijvers. « Robust random cut forest based anomaly detection on streams ». Dans International Conference on Machine Learning, pp. 2712-2721. 2016.

2. Byung-Hoon Park, George Ostrouchov, Nagiza F. Samatova et Al Geist. « Reservoir-based random sampling with replacement from data stream ». Dans Proceedings of the 2004 SIAM International Conference on Data Mining, pp. 492-496. Society for Industrial and Applied Mathematics, 2004.