モンテカルロドロップアウト

不確実性を推定する最も一般的な方法の 1 つは、ベイジアンニューラルネットワークを使用して予測分布を推測することです。予測分布を表すには、以下を使用します。

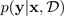
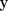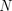
ターゲット 、インプット 、 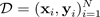および多数のトレーニング例を含む。予測分布が得られれば、分散を調べ、不確実性を明らかにすることができます。予測分布を学習する方法の 1 つは、関数にわたる分布、またはそれと同等にパラメーターにわたる分布 (パラメトリック事後分布 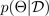) を学習する必要があります。

モンテカルロ (MC) のドロップアウト手法 (Gal and Ghahramani 2016) は、予測分布をスケーラブルに学習する方法です。MC ドロップアウトは、ニューラルネットワーク内のニューロンをランダムにオフにし、ネットワークを正則化することで機能します。各ドロップアウト構成は、おおよそのパラメトリック事後分布 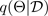とは異なるサンプルに対応しています：

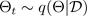
ここで 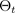は、次の図に示すように、近似的なパラメトリック事後分布 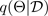からサンプリングされたドロップアウト構成、あるいは等価的にシミュレーション～に対応します。近似事後分布 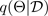からサンプリングすることで、モデルの可能性のモンテカルロ積分が可能になり、次のように予測分布が明らかになります。

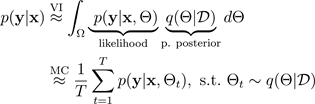
わかりやすくするために、確率はガウス分布であると仮定できます。

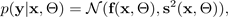
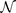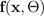ガウス関数 は、平均 と分散 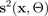のパラメータで指定され、モンテカルロドロップアウトBNNのシミュレーションによって出力されます：

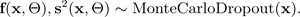
次の図は、MC ドロップアウトを示しています。各ドロップアウト構成では、順方向伝播のたびにニューロンのオフ (灰色の円) とオン (黒い円) がランダムに切り替わり、異なる出力が得られます。ドロップアウト構成が異なる複数のフォワードパスでは、平均 p(f(x, ø)) にわたる予測分布が得られます。

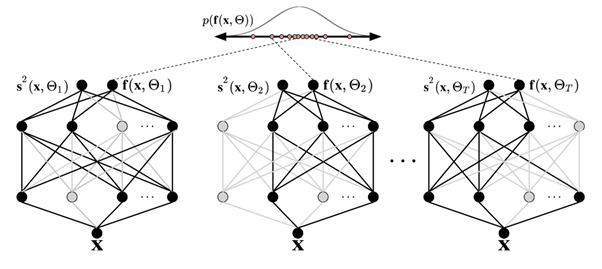
データを通過するフォワードパスの数は定量的に評価する必要がありますが、考慮すべき適切な範囲は 30 ～ 100 です (Gal and Ghahramani 2016)。