Monte Carlo 드롭아웃 - AWS 권장 가이드

기계 번역으로 제공되는 번역입니다. 제공된 번역과 원본 영어의 내용이 상충하는 경우에는 영어 버전이 우선합니다.

Monte Carlo 드롭아웃

불확실성을 추정하는 가장 일반적인 방법 중 하나는 Bayesian 신경망으로 예측 분포를 추론하는 것입니다. 예측 분포를 나타내려면 다음을 사용하십시오.

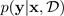
예측적 분포

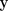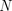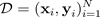목표 AWS logo with "Amazon Web Services" text on a white background. , 입력 X icon, typically used to represent closing or canceling an action. 및 Lambda function icon with a stylized λ (lambda) symbol in orange. 다양한 교육 예제 Mathematical formula showing D as a set of pairs (x_i, y_i) from i=1 to n. 가 포함되어 있습니다. 예측 분포를 구하면 분산을 검사하고 불확실성을 발견할 수 있습니다. 예측 분포를 학습하는 한 가지 방법은 함수에 대한 분포 또는 모수에 대한 분포(즉, 모수 사후 분포)를 학습하는 것입니다. 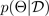Mathematical formula showing p(Θ|D) with vertical bar between Θ and D.

Monte Carlo (MC) 드롭아웃 기법(Gal과 Ghahramani 2016)은 예측 분포를 학습할 수 있는 확장 가능한 방법을 제공합니다. MC 드롭아웃은 신경망의 뉴런을 무작위로 차단하여 네트워크를 정규화하는 방식으로 작동합니다. 각 드롭아웃 구성은 근사 모수 사후 분포 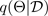Mathematical formula showing q(θ|D) representing a probability distribution. 와 다른 표본에 해당합니다.

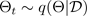
MC 드롭아웃

다음 그림과 같이 대략적인 사후 파라미터 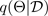Mathematical formula showing q(θ|D) representing a probability distribution. 에서 샘플링한 드롭아웃 구성 또는 시뮬레이션 ~에 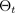Greek letter theta subscript i, representing a mathematical variable or symbol. 이 해당하는 경우 근사 사후 분포 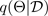Mathematical formula showing q(θ|D) representing a probability distribution. 에서 샘플링하면 Monte Carlo에서 모델 가능성을 통합하여 다음과 같이 예측 분포를 파악할 수 있습니다.

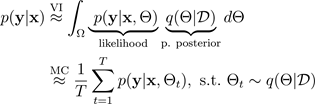
MC 드롭아웃에서의 예측 분포

단순화를 위해 확률을 가우스 분포로 가정할 수 있습니다.

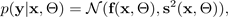
가우스 분산 가능성

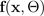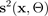Monte Carlo 드롭아웃 BNN의 시뮬레이션을 통해 출력되는 평균 Mathematical function f(x, θ) with x and θ as variables. 및 분산 Mathematical formula showing s prime as a function of x and theta. 파라미터수로 지정된 Mathematical equation showing N subscript V, representing a variable in a formula. 가우스 함수를 사용하는 경우

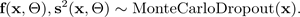
MC 드롭아웃 BNN

다음 그림에서는 MC 드롭아웃을 보여줍니다. 각 드롭아웃 구성은 순방향 전파마다 뉴런을 무작위로 끄고(회색 원) 켜짐(검은색 원)으로 전환하여 서로 다른 출력을 생성합니다. 드롭아웃 구성이 서로 다른 포워드 패스를 여러 번 사용하면 평균 p(f(x, ø))에 대한 예측 분포가 산출됩니다.

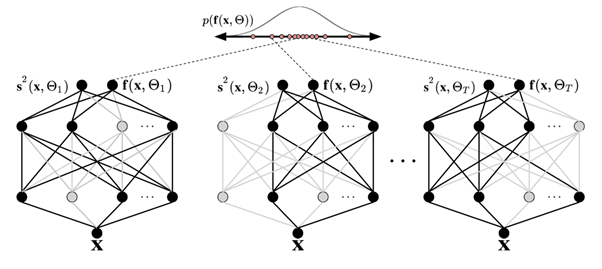
MC 드롭아웃

데이터를 통과하는 포워드 패스 횟수는 정량적으로 평가해야 하지만, 30-100은 고려하기에 적절한 범위입니다(Gal과 Ghahramani 2016).