4단계: 예측 변수 평가

기계 학습의 일반적인 워크플로는 훈련 세트에서 모델 세트 또는 모델 조합을 트레이닝하고 홀드아웃 데이터 세트에서 정확도를 평가하는 것으로 구성됩니다. 이 섹션에서는 과거 데이터를 분할하는 방법과 시계열 예측에서 모델을 평가하는 데 사용할 지표에 대해 설명합니다. 예측의 경우 백테스트 기법은 예측 정확도를 평가하는 주요 도구입니다.

백테스트

적절한 평가 및 백테스트 프레임워크는 기계 학습 애플리케이션을 성공으로 이끄는 가장 중요한 요소 중 하나입니다. 모델의 성공적인 백테스트를 통해 모델의 미래 예측력에 대한 확신을 얻을 수 있습니다. 또한 하이퍼파라미터 최적화(HPO)를 통해 모델을 조정하고, 모델 조합을 학습하고, 메타 학습 및 AutoML을 활성화할 수 있습니다.

시계열 예측 특성 시간은 평가 및 백테스트 방법론 측면에서 응용 기계 학습의 다른 분야와 차별화됩니다. 일반적으로 ML 작업에서는 백테스트의 예측 오류를 평가하기 위해 데이터 세트를 항목별로 분할합니다. 예를 들어 이미지 관련 작업의 교차 검증을 위해 사진의 일정 비율을 학습시킨 다음 다른 부분을 테스트 및 검증에 사용합니다. 예측을 할 때는 주로 시간별로(항목별로 낮게) 구분해서 훈련 세트의 정보가 테스트 또는 검증 세트로 유출되지 않도록 하고 생산 사례를 최대한 가깝게 시뮬레이션해야 합니다.

한 시점을 선택하는 것이 아니라 여러 지점을 선택하려면 시간별 분할을 신중하게 수행해야 합니다. 그렇지 않으면 분할 지점으로 정의된 예측 시작 날짜에 따라 정확도가 너무 크게 좌우됩니다. 여러 시점에 걸쳐 일련의 분할을 수행하고 평균 결과를 출력하는 롤링 예측 평가를 통해 더욱 강력하고 신뢰할 수 있는 백테스트 결과를 얻을 수 있습니다. 다음 그림은 네 가지 다른 백테스트 분할을 보여줍니다.

학습 세트 크기는 증가하지만 테스트 크기는 일정하게 유지되는 네 가지 백테스트 시나리오의 그림

위 그림에서 모든 백테스트 시나리오에는 예측된 값을 실제 값과 비교하여 평가할 수 있는 전체 데이터가 포함되어 있습니다.

여러 개의 백테스트 창이 필요한 이유는 실제 세계의 대부분의 시계열이 일반적으로 고정되지 않기 때문입니다. 북미에 기반을 둔 사례 연구의 전자 상거래 비즈니스는 제품 수요의 대부분이 4분기 성수기에 주도되며 특히 추수감사절과 크리스마스 이전에 최고조에 달합니다. 4분기 쇼핑 시즌에는 시계열 변동성이 해당 연도의 나머지 시기보다 높습니다. 여러 개의 백테스트 창을 통해 보다 균형 잡힌 환경에서 예측 모델을 평가할 수 있습니다.

다음 그림은 각 백테스트 시나리오에 대한 Amazon Forecast 용어의 기본 요소를 보여줍니다. Amazon Forecast는 자동으로 데이터를 학습 및 테스트 데이터 세트로 분할합니다. Amazon Forecast는 create_predictor API에서 파라미터로 지정되거나 기본값인 ForecastHorizon을 사용하는 BackTestWindowOffset 파라미터를 사용하여 입력 데이터를 분할하는 방법을 결정합니다.

다음 그림에서는BackTestWindowOffset 및ForecastHorizon 매개변수가 같지 않은 보다 일반적인 전자의 경우를 볼 수 있습니다. 이 BackTestWindowOffset 매개변수는 가상 예측 시작 날짜를 정의하며, 다음 그림에서 수직 점선으로 표시됩니다. '이 날 모델을 배포할 경우 예측치는 어떻게 될까요?'와 같은 가상의 질문에 답하는 데 사용할 수 있습니다. ForecastHorizon은 가상 예측 시작 날짜부터 예측까지 걸리는 시간 단계 수를 정의합니다.

Amazon Forecast에서의 단일 백테스트 시나리오 및 해당 구성 그림

Amazon Forecast는 백테스트 중에 생성된 예측값과 정확도 지표를 내보낼 수 있습니다. 내보낸 데이터는 특정 시점 및 분위에서 특정 항목을 평가하는 데 사용할 수 있습니다.

예측 분위 및 정확도 지표

예측 분위는 예측의 상한과 하한을 제공할 수 있습니다. 예를 들어, 예측 유형 0.1(P10), 0.5(P50) 및 0.9(P90)를 사용하면 P50 예측에 대한 80% 신뢰 구간이라고 하는 값 범위가 제공됩니다. P10, P50, P90에서 예측을 생성하면 실제 값이 80% 의 확률로 해당 경계 사이에 있을 것으로 예상할 수 있습니다.

이 백서에서는 5단계의 분위에 대해 더 자세히 설명합니다.

Amazon Forecast는 가중 분위 손실(wQL), 평균 제곱근 오차(RMSE) 및 가중 절대 백분율 오차(WAPE) 정확도 지표를 사용하여 백테스트 중에 예측기를 평가합니다.

가중 분위 손실(wQL)

가중 분위 손실(wQL) 오류 지표는 지정된 분위에서의 모델 예측 정확도를 측정합니다. 과소 예측과 과대 예측에 따른 비용이 서로 다를 때 특히 유용합니다. wQL 함수의 가중치 (τ)를 설정하면 과소 예측과 과대 예측에 대한 서로 다른 페널티가 자동으로 적용됩니다.

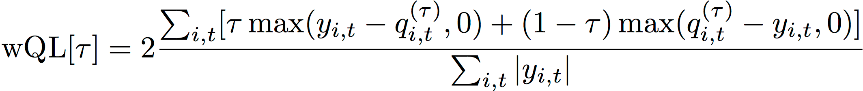
wQL 함수

여기서 각 항목은 다음과 같습니다.

• τ - {0.01, 0.02,..., 0.99} 집합 내의 분위

• qi,t(τ) - 모형이 예측하는 τ-분위

• yi, t - (i, t) 지점에서의 관측값

가중 절대 백분율 오차(WAPE)

가중 절대 백분율 오차(WAPE)는 모델 정확도를 측정하는 데 일반적으로 사용되는 지표입니다. 예측값과 관측값의 전체 편차를 측정합니다.

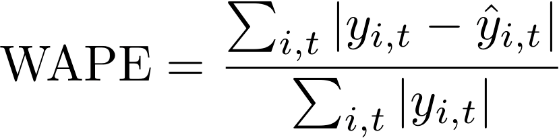
WAPE

여기서 각 항목은 다음과 같습니다.

• yi, t - (i, t) 지점에서의 관측값

• ŷi, t - (i, t) 지점에서의 예측값

예측은 평균 예측값을 예측값인 ŷi,t로 사용합니다.

평균 제곱근 오차(RMSE)

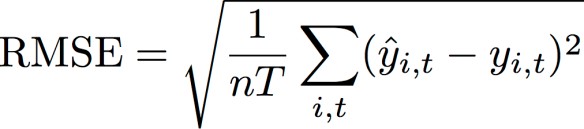
평균 제곱근 오차(RMSE)는 모델 정확도를 측정하는 데 일반적으로 사용되는 지표입니다. WAPE와 마찬가지로 관측값에서 추정치의 전체 편차를 측정합니다.

여기서 각 항목은 다음과 같습니다.

• yi, t - (i, t) 지점에서의 관측값

• ŷi, t - (i, t) 지점에서의 예측값

• nT - 테스트 세트의 데이터 포인트 수

예측은 평균 예측값을 예측값인 ŷi,t로 사용합니다. 예측 변수 지표를 계산할 때 nT는 백테스트 창의 데이터 포인트 수입니다.

WAPE 및 RMSE의 문제점

대부분의 경우 내부적으로 또는 다른 예측 도구를 통해 생성할 수 있는 포인트 예측은 p50 분위 또는 평균 예측과 일치해야 합니다. WAPE와 RMSE 모두에 대해 Amazon Forecast는 평균 예측을 사용하여 예측값 (yhat) 을 나타냅니다.

wQL[tau] 방정식의 tau = 0.5인 경우 두 가중치가 동일하며 wQL[0.5]은 포인트 예측에 일반적으로 사용되는 가중 절대 백분율 오차(WAPE)로 감소합니다.

여기서 yhat = q(0.5) 는 계산된 예측값입니다. wQL 공식에서 배율 인수 2는 0.5 인수를 상쇄하여 정확한 WAPE[중앙값] 식을 구하는 데 사용됩니다.

참고로 위의 WAPE 정의는 평균 절대 백분율 오차(MAPE)에 대한 일반적인 해석과 다릅니다. 차이점은 분모에 있습니다. 위에서 정의한 WAPE를 사용하면 사례 연구의 전자 상거래 비즈니스와 같은 실제 시나리오에서 흔히 발생하는 문제인 0으로 나누는 문제를 피할 수 있습니다. 이러한 문제는 특정 날짜에 특정 SKU를 0개 판매하는 경우가 많습니다.

0.5가 아닌 tau에 대한 가중 분위 손실 지표와 달리 가중치가 동일한 WAPE와 같은 계산으로는 각 분위의 고유한 편향을 포착할 수 없습니다. WAPE의 다른 단점은 대칭적이지 않고, 작은 숫자에 대한 백분율 오차가 과도하게 늘어나며, 점 단위 지표에 불과하다는 것입니다.

RMSE는 WAPE의 오차 항의 제곱이며 다른 ML 애플리케이션의 일반적인 오차 지표입니다. RMSE 지표는 개별적인 오차의 크기가 일정한 모델을 선호합니다. 오차의 변동이 커지면 RMSE가 과도하게 커지기 때문입니다. 오차의 제곱근이기 때문에 그렇지 않았다면 양호한 예상에서 몇 개의 잘못 예측된 값이 RMSE를 증가시킬 수 있습니다. 또한 제곱 항으로 인해 오차 항이 작을수록 WAPE보다 RMSE에서 가중치가 작아집니다.

정확도 지표를 통해 예측을 정량적으로 평가할 수 있습니다. 특히 대규모 비교(방법 A가 방법 B보다 전체적으로 우수한지 등)의 경우 이는 매우 중요합니다. 그러나 개별 SKU에 대한 시각 자료로 이를 보완하는 것이 중요한 경우가 많습니다.