Integração de Monte Carlo

Uma das formas mais populares de estimar a incerteza é inferir distribuições preditivas com redes neurais bayesianas. Para denotar uma distribuição preditiva, use:

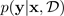
com metas 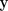, informações e 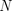muitos exemplos de treinamento 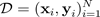. Ao obter uma distribuição preditiva, você pode inspecionar a variância e descobrir incertezas. Uma forma de aprender uma distribuição preditiva requer aprender uma distribuição sobre funções ou, equivalentemente, uma distribuição sobre os parâmetros (ou seja, a distribuição paramétrica posterior .

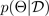A técnica de integração de Monte Carlo (MC) (Gal e Ghahramani 2016) fornece uma maneira escalável de aprender uma distribuição preditiva. A integração de MC funciona desligando aleatoriamente os neurônios em uma rede neural, o que regulariza a rede. Cada configuração de integração corresponde a uma amostra diferente da distribuição posterior paramétrica aproximada :

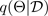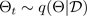
onde 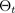corresponde a uma configuração de integração, ou, equivalentemente, a uma simulação ~, amostrada a partir da posterior paramétrica aproximada 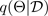, conforme mostrado na figura a seguir. A amostragem da parte posterior aproximada 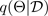permite a integração de Monte Carlo da probabilidade do modelo, o que revela a distribuição preditiva, da seguinte forma:

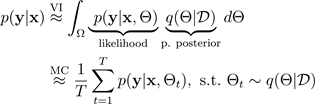
Para simplificar, pode-se presumir que a probabilidade seja distribuída gaussiana:

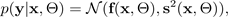
com a função gaussiana 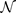especificada pelos parâmetros de média 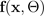e variância 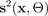, que são gerados por simulações do BNN de integração de Monte Carlo:

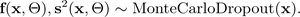
A figura a seguir mostra a integração de MC. Cada configuração de integração produz uma saída diferente ao desligar aleatoriamente os neurônios (círculos cinza) e ativá-los (círculos pretos) a cada propagação direta. Múltiplas passagens diretas com diferentes configurações de integração produzem uma distribuição preditiva sobre a média p(f(x, ø)).

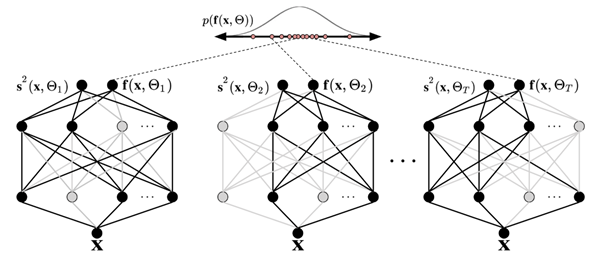
O número de passagens diretas pelos dados deve ser avaliado quantitativamente, mas 30 a 100 é um intervalo apropriado a ser considerado (Gal e Ghahramani 2016).