How Factorization Machines Work
The prediction task for a Factorization Machines model is to estimate a function ŷ from a feature set xi to a target domain. This domain is real-valued for regression and binary for classification. The Factorization Machines model is supervised and so has a training dataset (xi,yj) available. The advantages this model presents lie in the way it uses a factorized parametrization to capture the pairwise feature interactions. It can be represented mathematically as follows:
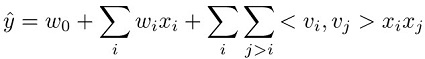
The three terms in this equation correspond respectively to the three components of the model:
-
The w0 term represents the global bias.
-
The wi linear terms model the strength of the ith variable.
-
The <vi,vj> factorization terms model the pairwise interaction between the ith and jth variable.
The global bias and linear terms are the same as in a linear model. The pairwise
feature interactions are modeled in the third term as the inner product of the
corresponding factors learned for each feature. Learned factors can also be considered
as embedding vectors for each feature. For example, in a classification task, if a pair
of features tends to co-occur more often in positive labeled samples, then the inner
product of their factors would be large. In other words, their embedding vectors would
be close to each other in cosine similarity. For more information about the
Factorization Machines model, see Factorization
Machines
For regression tasks, the model is trained by minimizing the squared error between the model prediction ŷn and the target value yn. This is known as the square loss:
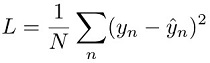
For a classification task, the model is trained by minimizing the cross entropy loss, also known as the log loss:

where:

For more information about loss functions for classification, see Loss functions
for classification