How PCA Works - Amazon SageMaker AI
Mode 1: RegularMode 2: Randomized

How PCA Works

Principal Component Analysis (PCA) is a learning algorithm that reduces the dimensionality (number of features) within a dataset while still retaining as much information as possible.

PCA reduces dimensionality by finding a new set of features called components, which are composites of the original features, but are uncorrelated with one another. The first component accounts for the largest possible variability in the data, the second component the second most variability, and so on.

It is an unsupervised dimensionality reduction algorithm. In unsupervised learning, labels that might be associated with the objects in the training dataset aren't used.

Given the input of a matrix with rows 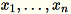x_1,…,x_n each of dimension 1 * d, the data is partitioned into mini-batches of rows and distributed among the training nodes (workers). Each worker then computes a summary of its data. The summaries of the different workers are then unified into a single solution at the end of the computation.

Modes

The Amazon SageMaker AI PCA algorithm uses either of two modes to calculate these summaries, depending on the situation:

  • regular: for datasets with sparse data and a moderate number of observations and features.

  • randomized: for datasets with both a large number of observations and features. This mode uses an approximation algorithm.

As the algorithm's last step, it performs the singular value decomposition on the unified solution, from which the principal components are then derived.

Mode 1: Regular

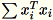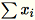The workers jointly compute both Equation in text-form: \sum x_i^T x_i and Equation in text-form: \sum x_i .

Note

Because 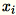Equation in text-form: x_i are 1 * d row vectors, 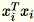Equation in text-form: x_i^T x_i is a matrix (not a scalar). Using row vectors within the code allows us to obtain efficient caching.

The covariance matrix is computed as 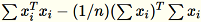Equation in text-form: \sum x_i^T x_i - (1/n) (\sum x_i)^T \sum x_i , and its top num_components singular vectors form the model.

Note

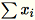If subtract_mean is False, we avoid computing and subtracting Equation in text-form: \sum x_i .

Use this algorithm when the dimension d of the vectors is small enough so that Equation in text-form: d^2 can fit in memory.

Mode 2: Randomized

When the number of features in the input dataset is large, we use a method to approximate the covariance metric. For every mini-batch 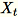Equation in text-form: X_t of dimension b * d, we randomly initialize a (num_components + extra_components) * b matrix that we multiply by each mini-batch, to create a (num_components + extra_components) * d matrix. The sum of these matrices is computed by the workers, and the servers perform SVD on the final (num_components + extra_components) * d matrix. The top right num_components singular vectors of it are the approximation of the top singular vectors of the input matrix.

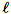
Let Equation in text-form: \ell = num_components + extra_components. Given a mini-batch 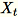Equation in text-form: X_t of dimension b * d, the worker draws a random matrix 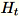Equation in text-form: H_t of dimension Equation in text-form: \ell * b . Depending on whether the environment uses a GPU or CPU and the dimension size, the matrix is either a random sign matrix where each entry is +-1 or a FJLT (fast Johnson Lindenstrauss transform; for information, see FJLT Transforms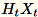 and the follow-up papers). The worker then computes Equation in text-form: H_t X_t and maintains 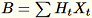Equation in text-form: B = \sum H_t X_t . 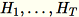The worker also maintains Equation in text-form: h^T , the sum of columns of Equation in text-form: H_1,..,H_T (T being the total number of mini-batches), and s, the sum of all input rows. After processing the entire shard of data, the worker sends the server B, h, s, and n (the number of input rows).

Denote the different inputs to the server as 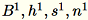Equation in text-form: B^1, h^1, s^1, n^1,… The server computes B, h, s, n the sums of the respective inputs. It then computes 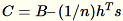Equation in text-form: C = B – (1/n) h^T s , and finds its singular value decomposition. The top-right singular vectors and singular values of C are used as the approximate solution to the problem.