How Tensor Parallelism Works
Tensor parallelism takes place at the level of nn.Modules; it
partitions specific modules in the model across tensor parallel ranks. This is in
addition to the existing partition of the set of
modules used in pipeline parallelism.
When a module is partitioned through tensor parallelism, its forward and backward propagation are distributed. The library handles the necessary communication across devices to implement the distributed execution of these modules. The modules are partitioned across multiple data parallel ranks. Contrary to the traditional distribution of workloads, each data parallel rank does not have the complete model replica when the library’s tensor parallelism is used. Instead, each data parallel rank may have only a partition of the distributed modules, in addition to the entirety of the modules that are not distributed.
Example: Consider tensor parallelism across data parallel ranks, where the degree of data parallelism is 4 and the degree of tensor parallelism is 2. Assume that you have a data parallel group that holds the following module tree, after partitioning the set of modules.
A ├── B | ├── E | ├── F ├── C └── D ├── G └── H
Assume that tensor parallelism is supported for the modules B, G, and H. One possible outcome of tensor parallel partition of this model could be:
dp_rank 0 (tensor parallel rank 0): A, B:0, C, D, G:0, H dp_rank 1 (tensor parallel rank 1): A, B:1, C, D, G:1, H dp_rank 2 (tensor parallel rank 0): A, B:0, C, D, G:0, H dp_rank 3 (tensor parallel rank 1): A, B:1, C, D, G:1, H
Each line represents the set of modules stored in that dp_rank, and
the notation X:y represents the yth fraction of the module
X. Note the following:
-
Partitioning takes place across subsets of data parallel ranks, which we call
TP_GROUP, not the entireDP_GROUP, so that the exact model partition is replicated acrossdp_rank0 anddp_rank2, and similarly acrossdp_rank1 anddp_rank3. -
The modules
EandFare no longer part of the model, since their parent moduleBis partitioned, and any execution that is normally a part ofEandFtakes place within the (partitioned)Bmodule. -
Even though
His supported for tensor parallelism, in this example it is not partitioned, which highlights that whether to partition a module depends on user input. The fact that a module is supported for tensor parallelism does not necessarily mean it is partitioned.
How
the library adapts tensor parallelism to PyTorch nn.Linear
module
When tensor parallelism is performed over data parallel ranks, a subset of the
parameters, gradients, and optimizer states are partitioned across the tensor
parallel devices for the modules that are
partitioned. For the rest of the modules, the tensor parallel
devices operate in a regular data parallel manner. To execute the partitioned
module, a device first collects the necessary parts of all data samples across peer devices in the same tensor
parallelism group. The device then runs the local fraction of the module on all
these data samples, followed by another round of synchronization which both
combines the parts of the output for each data sample and returns the combined
data samples to the GPUs from which the data sample first originated. The
following figure shows an example of this process over a partitioned
nn.Linear module.
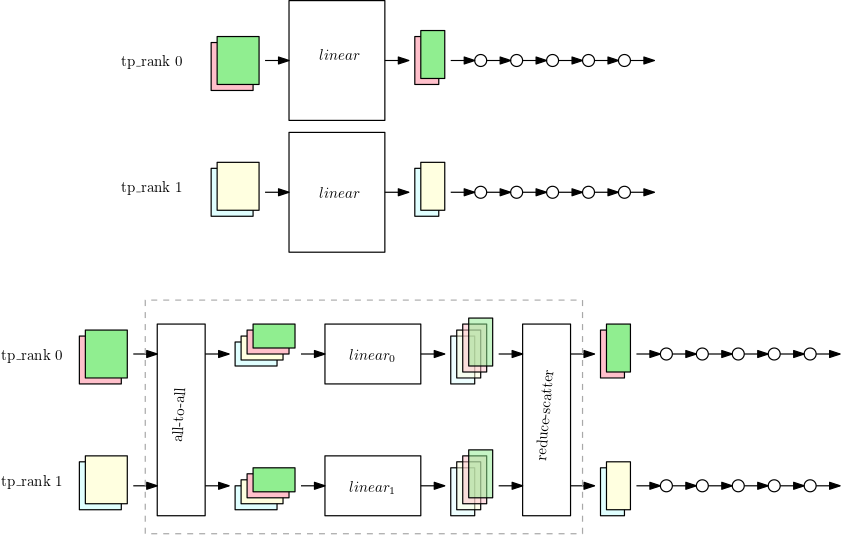
The first figure shows a small model with a large nn.Linear
module with data parallelism over the two tensor parallelism ranks. The
nn.Linear module is replicated into the two parallel ranks.
The second figure shows tensor parallelism applied on a larger model while
splitting the nn.Linear module. Each tp_rank holds
half the linear module, and the entirety of the rest of the operations. While
the linear module runs, each tp_rank collects the relevant half of
all data samples and passes it through their half of the nn.Linear
module. The result needs to be reduce-scattered (with summation as the reduction
operation) so that each rank has the final linear output for their own data
samples. The rest of the model runs in the typical data parallel manner.