概述

关于什么是可解释模型或者哪些信息足以作为模型的解释，尚无普遍接受的定义。本指南侧重于常用的特征重要性概念，其中使用每个输入特征的重要性分数解释该输入特征如何影响模型输出。这种方法可以提供见解，但也需要谨慎行事。特征重要性分数可能有误导性，并且应仔细分析，包括尽可能偕同主题专家验证。具体而言，我们建议您在未验证情况下勿信任特征重要性分数，因为错误解释可能导致不良业务决策。

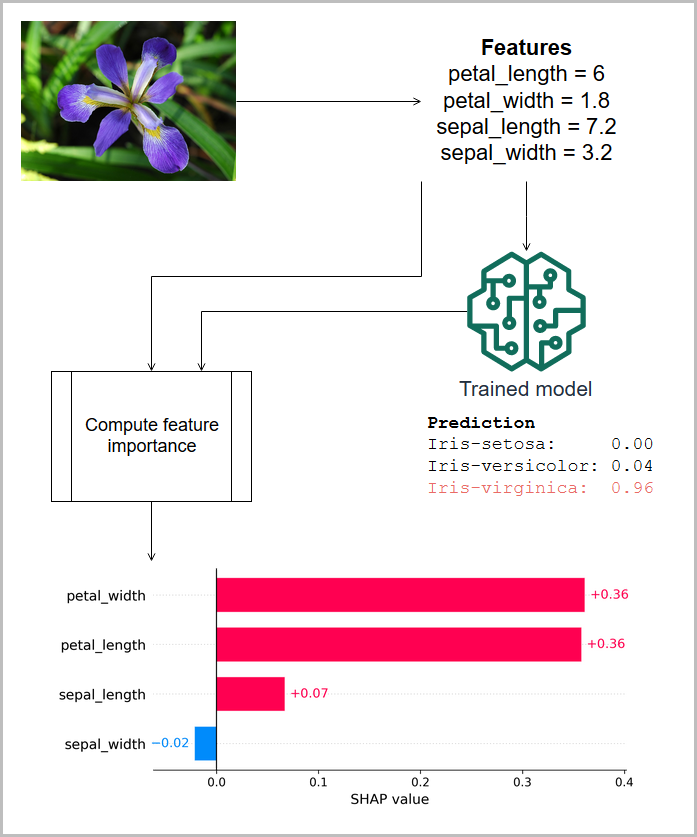
在下示图中，将鸢尾的实测特征送入预测植物物种的模型，并且显示这种预测的相关特征重要性（SHAP 属性）。在这种情况下，花瓣长度、花瓣宽度和萼片长度都正向促成弗吉尼亚鸢尾分类，但萼片宽度有负向贡献。（此信息基于来自 [4] 的鸢尾数据集。）

特征重要性分数可以为全局性，表示该分数跨所有输入对模型有效，或为局部性，表示该分数适用于单一模型输出。局部特征重要性分数往往经缩放及求和以产生模型输出值，因此称为归因。简单模型被认为更可解释，因为输入特征对模型输出的影响更易理解。例如，在线性回归模型中，系数的大小提供了全局特征重要性分数，而对于给定的预测，局部特征归因是其系数和特征值的乘积。在缺少某预测的直接局部特征重要性分数情况下，您可以从一组基线输入特征中计算重要性分数，以了解某特征如何相对于基线做出贡献。