蒙特卡洛辍学

估计不确定性的最常用方法之一是使用贝叶斯神经网络推断预测分布。欲表示预测分布，请使用：

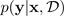
包括目标 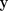、输入 和 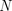许多训练示例 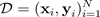。获得预测分布后，您可以检查方差并发现不确定性。学习预测分布的一种方法是学习函数上的分布，或者等效地，学习参数上的分布（即参数后验分布） 。

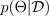蒙特卡洛（MC）辍学技术（Gal and Ghahramani 2016）为学习预测分布提供了一种可扩展的方法。MC dropout 的工作原理是随机关闭神经网络中的神经元，从而对网络进行正则化。每种 dropout 配置对应于与近似参数化后验分布不同的样本：

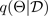
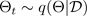
其中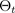， 对应于从近似参数化后验中抽样的掉线配置，或者等效地对应于模拟 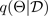，如下图所示。从近似后验中抽样 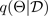可以对模型的似然进行蒙特卡洛积分，从而揭示预测分布，如下所示：

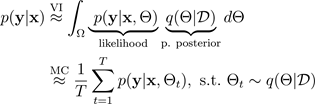
为简单起见，可以假设似然为高斯分布：

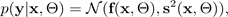
使用由均值 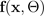和方差 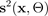参数指定的高斯函数 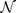，这些参数由蒙特卡洛辍学 BNN 的模拟输出：

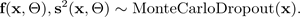
下图展示了MC dropout情况。每种 dropout 配置通过在每次向前传播时随机关闭神经元（灰色圆圈）和开启（黑色圆圈）来产生不同的输出。具有不同 dropout 配置的多次前向传递会产生平均值 p(f(x, ø)) 的预测分布。

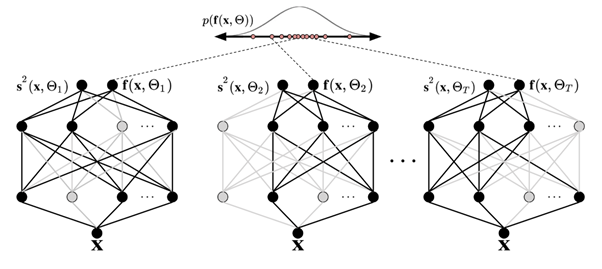
应定量评估通过数据的向前传递次数，但30-100是需要考虑的适当范围（Gal 和 Ghahramani， 2016年）。