Die vorliegende Übersetzung wurde maschinell erstellt. Im Falle eines Konflikts oder eines Widerspruchs zwischen dieser übersetzten Fassung und der englischen Fassung (einschließlich infolge von Verzögerungen bei der Übersetzung) ist die englische Fassung maßgeblich.
Funktionsweise der PCA
Die PCA ist ein unüberwachter Machine-Learning-Algorithmus, der die Dimensionalität (Anzahl der Merkmale) innerhalb eines Datensatzes reduziert und zugleich so viele Informationen wie möglich beibehält.
Die PCA reduziert die Dimensionalität, indem sie eine neue Menge an Merkmalen, sogenannter Komponenten, ermittelt, die Composites der ursprünglichen Merkmale sind, die jedoch nicht miteinander korrelieren. Die erste Komponente umfasst die größtmögliche Variabilität der Daten, die zweite Komponente die zweitgrößte Variabilität und so weiter.
Es handelt sich um eine unüberwachten Algorithmus zur Reduktion der Dimensionalität. Bei unüberwachtem Lernen werden Kennzeichnungen, die den Objekten im Trainingsdatensatz zugeordnet werden, nicht verwendet.
Angenommen es liegt eine Matrix mit den Zeilen
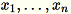 und der Dimension
und der Dimension 1 * d vor. Die Daten werden zeilenweise in Mini-Stapel partitioniert an das Trainingsknoten (Worker) verteilt. Jeder Worker berechnet eine Zusammenfassung seiner Daten. Die Zusammenfassungen der verschiedenen Worker werden am Ende der Berechnung in einer einzigen Lösung zusammengeführt.
Modi
Der Amazon SageMaker AI PCA-Algorithmus verwendet je nach Situation einen von zwei Modi, um diese Zusammenfassungen zu berechnen:
-
regular: bei Datensätzen mit geringer Datendichte und einer geringen Anzahl an Beobachtungen und Merkmalen.
-
randomized: bei Datensätzen mit einer großen Anzahl an Beobachtungen und Merkmalen. Dieser Modus verwendet einen Approximationsalgorithmus.
Der Algorithmus wendet als letzten Schritt die Singulärwertzerlegung für die vereinheitlichte Lösung an, von der die Hauptkomponenten abgeleitet werden.
Modus 1: regular
Die Worker berechnen sowohl
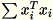 als auch
als auch
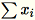 .
.
Anmerkung
Da
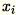
1 * d Zeilenvektoren sind, ist
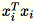 eine Matrix (keine Skalarfunktion). Das Verwenden von Vektoren innerhalb des Codes ermöglicht effizientes Caching.
eine Matrix (keine Skalarfunktion). Das Verwenden von Vektoren innerhalb des Codes ermöglicht effizientes Caching.
Die Kovarianzmatrix wird als
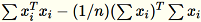 berechnet und die oberen
berechnet und die oberen num_components singulären Vektoren bilden das Modell.
Anmerkung
Wenn subtract_mean gleich False ist, wird auf die Berechnung und Subtraktion von
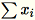 verzichtet.
verzichtet.
Verwenden Sie diesen Algorithmus, wenn die Dimension d der Vektoren klein genug ist, sodass
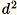 in den Arbeitsspeicher integriert werden kann.
in den Arbeitsspeicher integriert werden kann.
Modus 2: randomized
Wenn die Anzahl der Merkmale im eingegebenen Datensatz groß ist, wird eine Methode zur Approximierung der Kovarianzmetrik angewandt. Für jeden Mini-Stapel
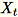 der Dimension
der Dimension b * d initialisieren wir nach dem Zufallsprinzip eine (num_components + extra_components) * b Matrix, die mit jedem Mini-Stapel multipliziert wird, um eine (num_components + extra_components) * d Matrix zu erstellen. Die Summe dieser Matrizes wird durch die Worker berechnet. Die Server wendet die Singulärwertzerlegung auf die letzte (num_components + extra_components) * d-Matrix an. Die singulären Vektoren num_components oben rechts sind die Approximation der obersten singulären Vektoren der Eingabematrix.
Nehmen wir an
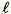
= num_components + extra_components. Mit einem gegebenen Mini-Stapel
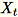 der Dimension
der Dimension b * d zeichnet der Worker zeichnet eine zufällige Matrix
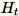 der Dimension
der Dimension
 . Je nachdem, ob die Umgebung eine GPU oder CPU verwendet und je nach Dimensionsgröße, ist die Matrix entweder eine randomisierte Matrix mit Vorzeichen, bei der jeder Eintrag
. Je nachdem, ob die Umgebung eine GPU oder CPU verwendet und je nach Dimensionsgröße, ist die Matrix entweder eine randomisierte Matrix mit Vorzeichen, bei der jeder Eintrag +-1 lautet, oder eine FJLT (schnelle Johnson-Lindenstrauss-Transformation). Weitere Informationen finden Sie unter FJLT Transforms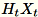 und behält
und behält
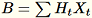 bei. Der Worker behält außerdem
bei. Der Worker behält außerdem
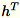 bei, die Summe der Spalten
bei, die Summe der Spalten
 (
(T ist die Gesamtanzahl der Mini-Stapel) und s, die Summe aller Eingabezeilen. Nach der Verarbeitung der gesamten Datenbruchstücke schickt der Worker B, h, s und n (die Anzahl der Eingabezeilen) an den Server.
Bezeichnen Sie die verschiedenen Eingaben an den Server als
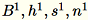 . Der Server berechnet
. Der Server berechnet B, h, s, n die Summen der jeweiligen Eingaben. Anschließend wird
 berechnet und seine Singulärwertzerlegung gesucht. Die oberen rechten singulären Vektoren und einzelne Werte von
berechnet und seine Singulärwertzerlegung gesucht. Die oberen rechten singulären Vektoren und einzelne Werte von C werden als Approximationslösung des Problems verwendet.