Terjemahan disediakan oleh mesin penerjemah. Jika konten terjemahan yang diberikan bertentangan dengan versi bahasa Inggris aslinya, utamakan versi bahasa Inggris.
Monte Carlo putus sekolah
Salah satu cara paling populer untuk memperkirakan ketidakpastian adalah dengan menyimpulkan distribusi prediktif dengan jaringan saraf Bayesian. Untuk menunjukkan distribusi prediktif, gunakan:
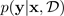
dengan target
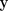 , masukan
, masukan
 , dan
, dan
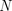 banyak contoh pelatihan
banyak contoh pelatihan
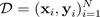 . Ketika Anda mendapatkan distribusi prediktif, Anda dapat memeriksa varians dan mengungkap ketidakpastian. Salah satu cara untuk mempelajari distribusi prediktif membutuhkan pembelajaran distribusi atas fungsi, atau, secara setara, distribusi di atas parameter (yaitu, distribusi posterior parametrik.
. Ketika Anda mendapatkan distribusi prediktif, Anda dapat memeriksa varians dan mengungkap ketidakpastian. Salah satu cara untuk mempelajari distribusi prediktif membutuhkan pembelajaran distribusi atas fungsi, atau, secara setara, distribusi di atas parameter (yaitu, distribusi posterior parametrik.

Teknik putus sekolah Monte Carlo (MC) (Gal dan Ghahramani 2016) menyediakan cara yang terukur untuk mempelajari distribusi prediktif. MC dropout bekerja dengan mematikan neuron secara acak di jaringan saraf, yang mengatur jaringan. Setiap konfigurasi putus sekolah sesuai dengan sampel yang berbeda dari perkiraan distribusi posterior parametrik:
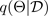
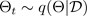
di mana
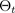 sesuai dengan konfigurasi putus sekolah, atau, setara, simulasi ~, diambil sampelnya dari perkiraan parametrik posterior
sesuai dengan konfigurasi putus sekolah, atau, setara, simulasi ~, diambil sampelnya dari perkiraan parametrik posterior
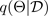 , seperti yang ditunjukkan pada gambar berikut. Pengambilan sampel dari perkiraan posterior
, seperti yang ditunjukkan pada gambar berikut. Pengambilan sampel dari perkiraan posterior
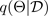 memungkinkan integrasi Monte Carlo dari kemungkinan model, yang mengungkap distribusi prediktif, sebagai berikut:
memungkinkan integrasi Monte Carlo dari kemungkinan model, yang mengungkap distribusi prediktif, sebagai berikut:

Untuk kesederhanaan, kemungkinan dapat diasumsikan terdistribusi Gaussian:
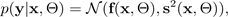
dengan fungsi Gaussian yang
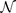 ditentukan oleh
ditentukan oleh
 parameter mean
parameter mean
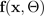 dan varians, yang dihasilkan oleh simulasi dari BNN putus sekolah Monte Carlo:
dan varians, yang dihasilkan oleh simulasi dari BNN putus sekolah Monte Carlo:
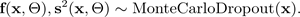
Gambar berikut menggambarkan putus sekolah MC. Setiap konfigurasi putus sekolah menghasilkan output yang berbeda dengan mematikan neuron secara acak (lingkaran abu-abu) dan hidup (lingkaran hitam) dengan setiap propagasi maju. Beberapa pass maju dengan konfigurasi putus sekolah yang berbeda menghasilkan distribusi prediktif di atas rata-rata p (f (x, ø)).
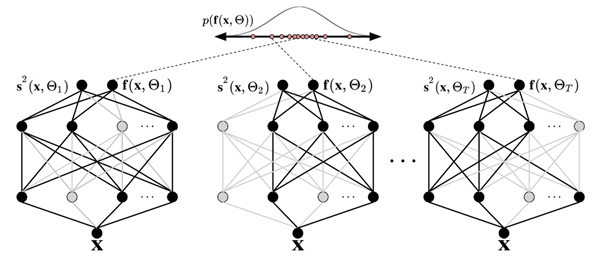
Jumlah forward pass melalui data harus dievaluasi secara kuantitatif, tetapi 30-100 adalah kisaran yang tepat untuk dipertimbangkan (Gal dan Ghahramani 2016).