Aleatoric uncertainty
Aleatoric uncertainty refers to the data’s inherent randomness that cannot be explained away
(aleator refers to someone who rolls the dice in Latin). Examples of data
with aleatoric uncertainty include noisy telemetry data and low-resolution images or social media
text. You can assume the aleatoric uncertainty
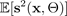, the inherent randomness, to be either constant
(homoscedastic) or variable (heteroscedastic), as a
function of the input explanatory variables.
Homoscedastic aleatoric uncertainty
Homoscedastic aleatoric uncertainty, when
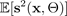is constant, is the simplest case and commonly encountered in regression
under the modeling assumption that
, where
, where
is the identity matrix and
is a constant scalar. It is highly restrictive to assume constant aleatoric
risk—to assume that noise
about a response
is independent from the explanatory variable
and constant—and rarely reflective of reality. Many phenomena in nature do
not exhibit constant randomness. For example, uncertainty about outcomes in physical systems,
such as fluid motion, are usually a function of kinetic energy. Consider the contrast between
the turbulent water flow of a large waterfall and the laminar water flow of a decorative
fountain. The stochasticity (randomness) of a water particle’s trajectory is a function of the
kinetic energy and therefore not constant. This assumption can lead to loss of valuable
information when modeling relationships between targets and inputs that host variable noise, and
cannot be explained with the observable information. As a consequence, in most cases, it is not
sufficient to assume homoscedastic uncertainty. Unless the phenomena is known to be
homoscedastic in nature, the inherent noise should be modeled as a function of the explanatory
variables
, if it can be done so.
Heteroscedastic aleatoric uncertainty
Heteroscedastic aleatoric uncertainty is when we consider the inherent randomness within
data to be a function of the data itself
. To calculate this type of uncertainty, you average a sample set of the
predictive variance:
with
being estimated by a BNN. Learning aleatoric uncertainty during training
encourages BNNs to encapsulate the inherent randomness within the data that can’t be explained
away. If there is no inherent randomness,
should tend toward zero.
