Decomposing uncertainty

Bayesian neural networks (BNNs) yield a predictive distribution , which provides a set of different predictions from which you can estimate variance ; that is, total predictive uncertainty . The total predictive uncertainty can be split into these two components of uncertainty by using the law of total variance:

The expected value of a target variable , given input and random parameters that specify a BNN, , is estimated by a BNN with a single forward propagation and denoted as . The variance of the target, given input and random parameters, , is output by the BNN, too, and denoted as . Thus, the total predictive uncertainty is the sum of these two numbers:

• The variance about the BNN’s predicted means — the epistemic uncertainty

• The average of the BNN’s predicted variance 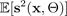— the aleatoric uncertainty

The following formula demonstrates how to calculate total uncertainty in accordance with (Kendall and Gal 2017). BNNs input , generate a random parameter configuration , and make a single forward propagation through the neural network to output a mean and variance . We denote a random generation, or simulation, by ~. With fixed , you can reiterate this process many times to yield a set:

These many samples provide the necessary statistics to ascertain uncertainties. You can do this by estimating epistemic uncertainty and aleatoric uncertainty separately, and then take their sum, as shown previously in the first equation in this section.