Temperature scaling

In classification problems, the predicted probabilities (softmax output) are assumed to represent the true correctness probability for the predicted class. However, although this assumption might have been reasonable for models a decade ago, it isn’t true for today’s modern neural network models (Guo et al. 2017). The loss of connection between model predicting probabilities and the confidence of model predictions would prevent the application of modern neural network models into real-world problems, as in decision-making systems. Precisely knowing the confidence score of model predictions is one of the most critical risk control settings required for building robust and trustworthy machine learning applications.

Modern neural network models tend to have large architectures with millions of learning parameters. The distribution of predicting probabilities in such models is often highly skewed to either 1 or 0, meaning that the model is overconfident and the absolute value of these probabilities could be meaningless. (This issue is independent of whether class imbalance is present in the dataset.) Various calibration methods for creating a prediction confidence score have been developed in the past ten years through post-processing steps to recalibrate the naïve probabilities of the model. This section describes one calibration method called temperature scaling, which is a simple yet effective technique for recalibrating prediction probabilities (Guo et al. 2017). Temperature scaling is a single-parameter version of Platt Logistic Scaling (Platt 1999).

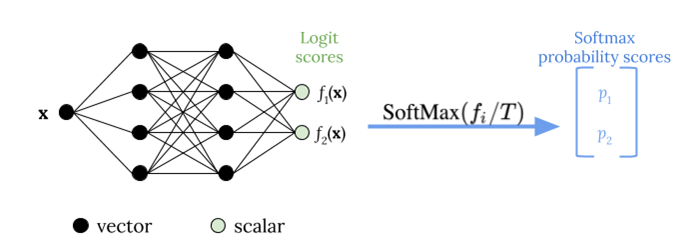
Temperature scaling uses a single scalar parameter T > 0, where T is the temperature, to rescale logit scores before applying the softmax function, as shown in the following figure. Because the same T is used for all classes, the softmax output with scaling has a monotonic relationship with unscaled output. When T = 1, you recover the original probability with the default softmax function. In overconfident models where T > 1, the recalibrated probabilities have a lower value than the original probabilities, and they are more evenly distributed between 0 and 1.

The method to get an optimal temperature T for a trained model is through minimizing the negative log likelihood for a held-out validation dataset.

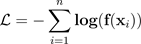
We recommend that you integrate the temperature scaling method as a part of the model training process: After a model training is completed, extract the temperature value T by using the validation dataset, and then rescale logit values by using T in the softmax function. Based on experiments in text classification tasks using BERT-based models, the temperature T usually scales between 1.5 and 3.

The following figure illustrates the temperature scaling method, which applies temperature value T before passing the logit score to the softmax function.

The calibrated probabilities by temperature scaling can approximately represent the confidence score of model predictions. This can be evaluated quantitatively by creating a reliability diagram (Guo et al. 2017), which represents the alignment between the distribution of expected accuracy and the distribution of predicting probabilities.

Temperature scaling has also been evaluated as an effective way to quantify total predictive uncertainty in the calibrated probabilities, but it is not robust in capturing epistemic uncertainty in scenarios like data drifts (Ovadia et al. 2019). Considering the ease of implementation, we recommend that you apply temperature scaling to your deep learning model output to build a robust solution for quantifying predictive uncertainties.